Machine Learning: from Theory to Practice
Author: TSINGHUA Computer Science & Finance Shiying Zhang 2021011056
Chapter0 Definition and Terms
人工智能 / Artificial Intelligence
计算机科学领域,专注于开发通常需要人类智能的任务,例如策略博弈、自然语言处理等
机器学习 / Machine Learning
是人工智能的一个子集,基于训练的算法(training algorithm),即对数据集进行学习和模式识别,从而进行预测或决策,而非对问题进行直接的人为编程
监督学习 / Supervised Learning:用于训练的数据集是标签的(labeled data)
- 回归问题 / Regression:Trees (Random Forests, GBM, DT / Decision Trees 决策树), Linear / GLMS, Ensemble, Neural Networks
- 分类问题 / Classification:SVM (支撑向量机 / Support Vector Machines), Discriminant Analysis, GNB (高斯朴素贝叶斯分类 / Gaussian Naïve Bayes) , Nearest Neighbor
无监督学习 / Unsupervised Learning:用于训练的数据集没有预先标签(unlabeled data)
聚类 / Clustering:K-Means (K-均值聚类), Gaussian Mixture Model (高斯混合模型), Hierarchical, Neural Networks
半监督学习 / Semi-Supervised Learning:同时使用标签的和未标签的数据集进行训练(algorithm 用 labeled data 识别模式,用 unlabeled data 进一步学习和理解模式)
self-training, generative models, S3VMs, Graph based algorithms, Multiview algorithms
强化学习 / Reinforcement Learning:根据环境反馈进行决策,通过trial and error学习
Markov Decision Process (MDP), Monte-Carlo Simulation (蒙特卡洛模拟)
深度学习 / Deep Learning:使用Artificial Neural Network的特定领域
全连接神经网络,卷积神经网络,循环神经网络
除此之外,机器学习还可以分为基于模型学习和基于实例学习:
- 基于模型学习 / Model-based Learning:对数据进行整体归纳提炼(从实例中构建模型,用模型进行预测)
- 基于实例学习 / Instance-based Learning:未对数据进行整体归纳提炼(学习示例,然后用相似度度量新的实例和已经学习的实例的关系,从而泛化新实例)
机器学习过程的两个阶段是训练(train / fit)和推断(inference / predict)
Chapter1 启发式搜索 Search
寻找起点s到终点g的最短路(最短耗散值)
引入:宽度优先搜索(BFS)+ Dijkstra算法、深度优先搜索(DFS)
1.1 A* 算法
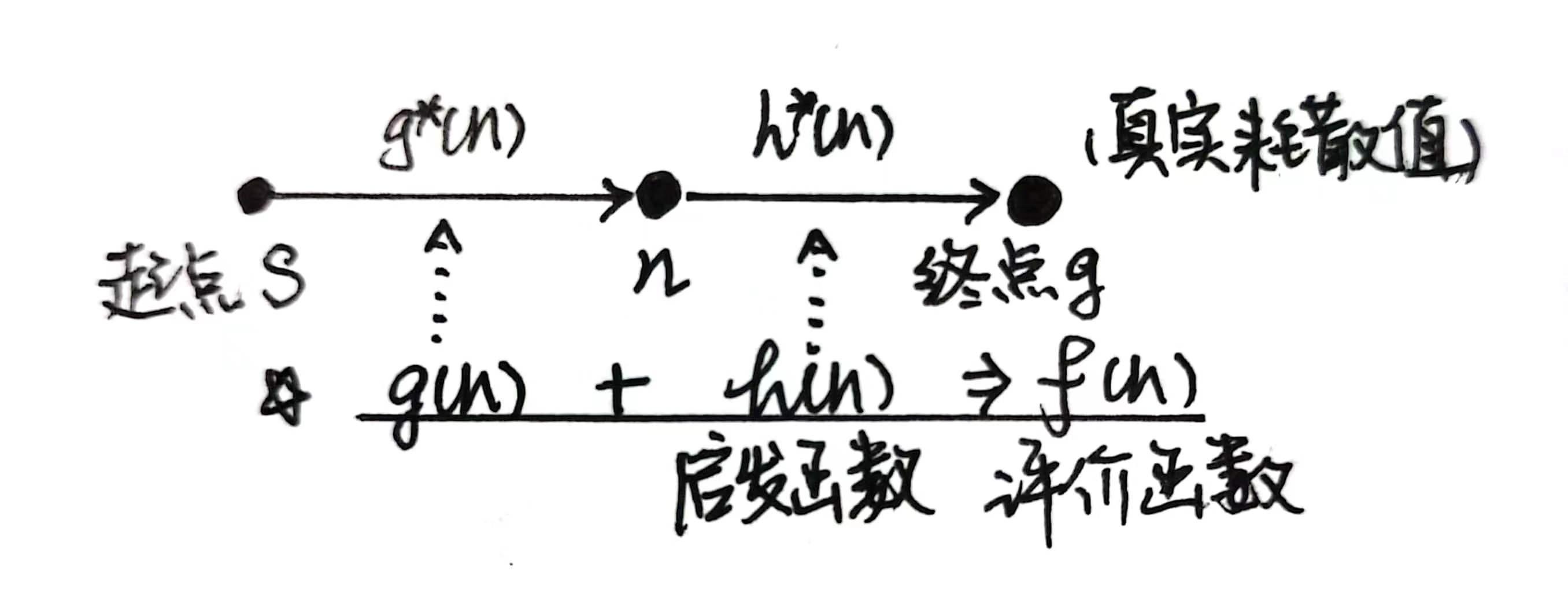
1. 伪代码及算法描述
优先扩展
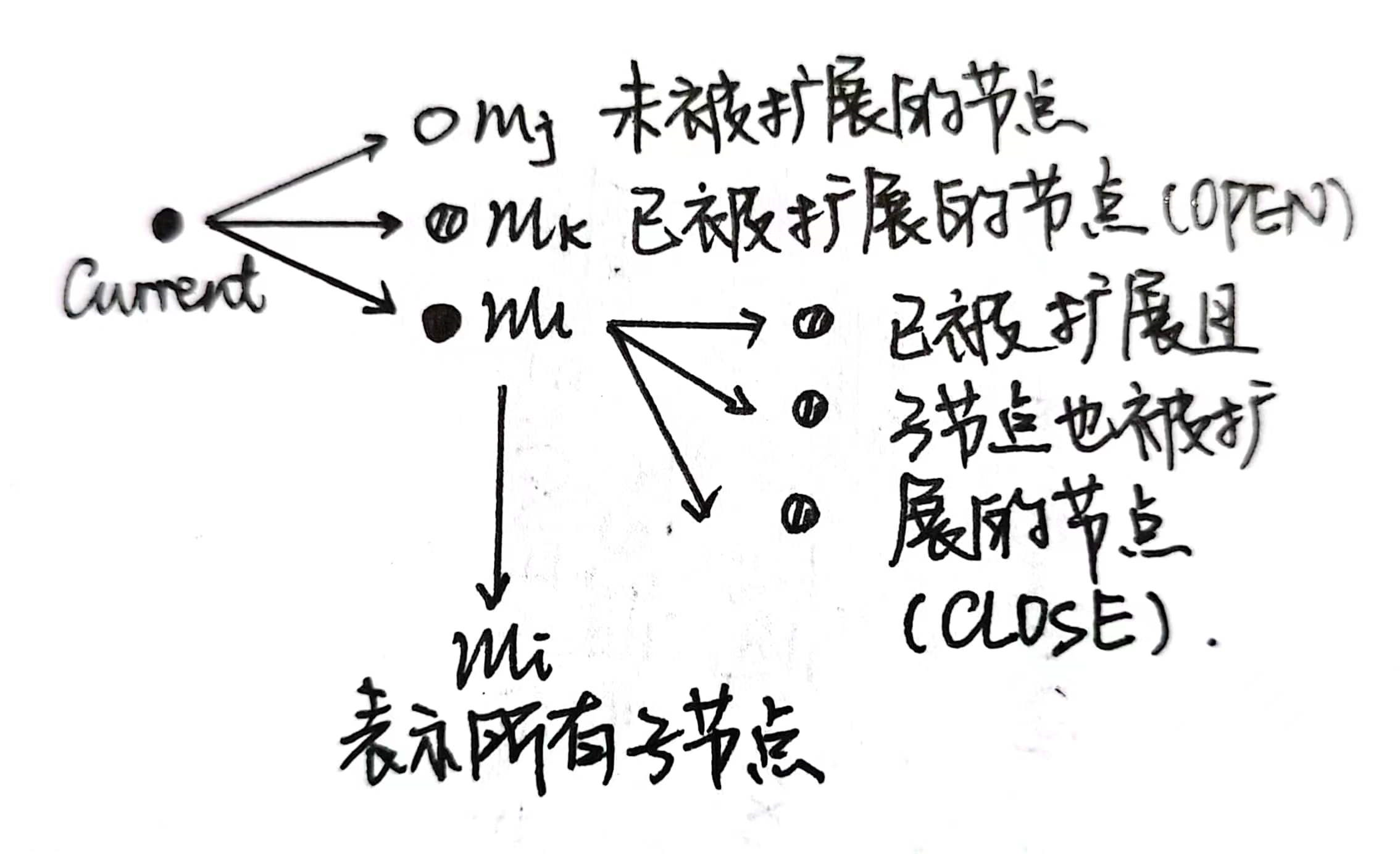
Notation:
:未被扩展的节点 :已被扩展的节点(OPEN表中) :已被扩展且子节点也被扩展的节点(CLOSED表中) :表示所有的子节点
算法:
举例:
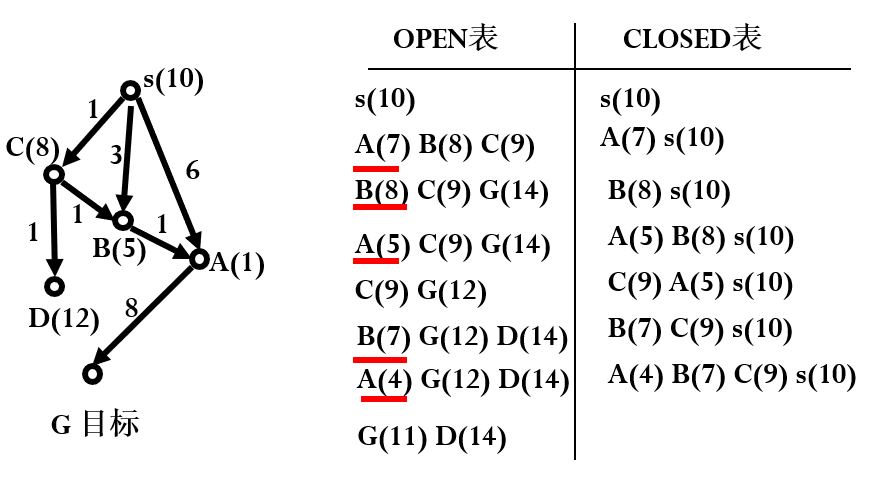
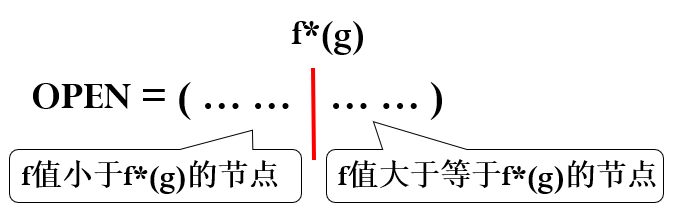
当g(n)更新时,
2. 算法分析
- 可采纳性定理:条件
s到重点g的路径) - 启发信息定理:如果
对启发函数
1.2 改进版A*算法
启发函数
则称启发函数
1. 伪代码及算法描述
Notation:
:到目前为止已扩展节点(即 表中的节点)的最大 值
算法:
举例:(注意,下例不满足启发函数单调性条件)

2. 算法分析
若
- 可以证明,当
- 可以证明,当
1.3 viterbi 算法
维特比算法(英语:Viterbi algorithm)是一种动态规划算法,它用于寻找最有可能产生观测事件序列的维特比路径——隐含状态序列
其中,动态转移方程如下:
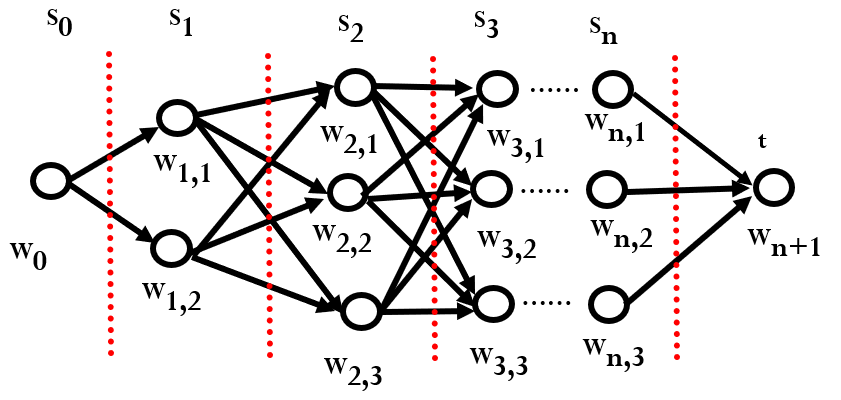
算法:
1. 汉字识别后处理
2. 拼音输入法
在拼音输入法的例子里,上式有
Chapter2 神经网络
神经网络的理论推导 + PyTorch语法实践
MLP / MultiLayer Perceptron(多层感知器神经网络): 由多层全连接神经网络(FCN / Fully-Connected Network)组成的 feed forward neural network,由 input layer,output layer 和 hidden layer 共同组成
CNN / Convolutional Neural Network(卷积神经网络):包含卷积计算且具有深度结构的 feed forward neural network,包括了input layer, convolutional layer, Relu layer, pooling layer and fully-connected / linear layer
RNN / Recurrent Neural Network(循环神经网络):以序列数据为输入,在序列的演进方向进行 recursion,且所有节点/循环单元按链式连接的 recursive neural network
- LSTM / Long Short-Term Memory(长短期记忆网络)
- GRU / Gated Recurrent Unit(门控循环单元)
2.1 全连接神经网络 MLP / FCN
结构:输入层(input layer)+ 若干隐含层(hidden layer)+ 输出层(output layer)
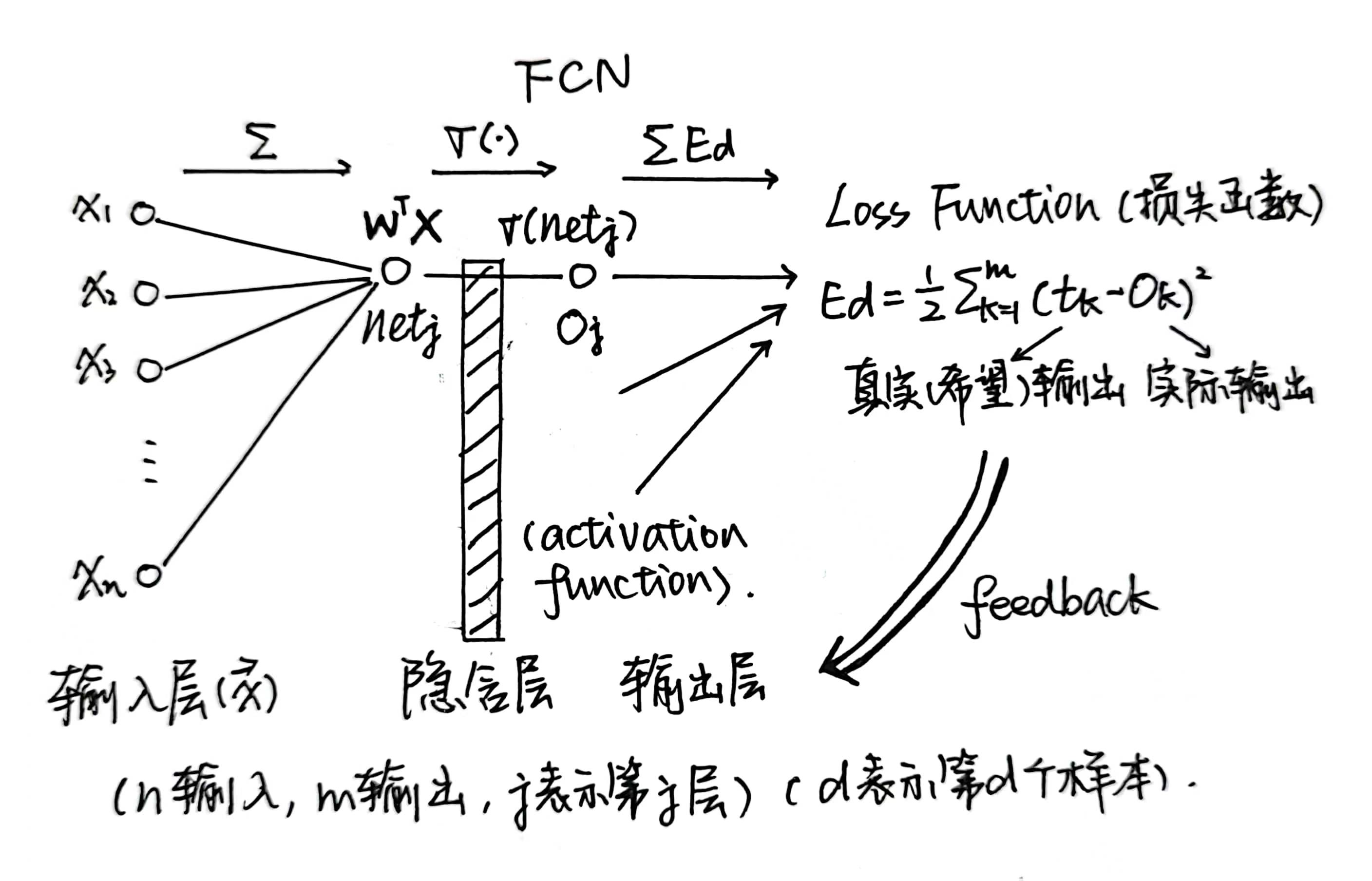
激活函数 Activation Function
符号函数:
损失函数 Loss Function
“误差平方和”损失函数
每次处理单个样本的误差:
小批量梯度下降算法:每次处理小批量(数量为
交叉熵损失函数
梯度下降法 Gradient Descent
反向传播 Back Propagation
算法过程:
理论推导:
Notations:
j(即那一层的第j个神经元)的第i个输入j(即那一层的第j个神经元)的第i个权重j计算的加权和,即输出层
隐含层
最靠近输出层的隐含层:
其它隐含层同上更新参数,
Softmax层:一般在输出层前采用Softmax函数转换为概率,可用于分类问题
2.2 卷积神经网络 CNN
结构:卷积层 + Relu层 + 池化层 + 全连接层等
【卷积层】一个
- 卷积核的大小:卷积核的大小决定了其参数量,上例参数量为
- 步长:卷积核每次移动的距离
- 采用填充的方式:使得每层得到的结果和大小和输入一致(这也是为什么大小是奇数) 比如:3*3填充1,5*5填充2
- (输出)通道数:即卷积核的个数 (输入)通道数:即卷积核的厚度
运算逻辑:矩阵对应相乘,各元素之和取平均 结果直观理解:越接近

- 卷积核的大小:卷积核的大小决定了其参数量,上例参数量为
【Relu层】非线性激活函数
Relu():保留 feature map 中大于等于0的值,其余所有小于0的数值直接改写为0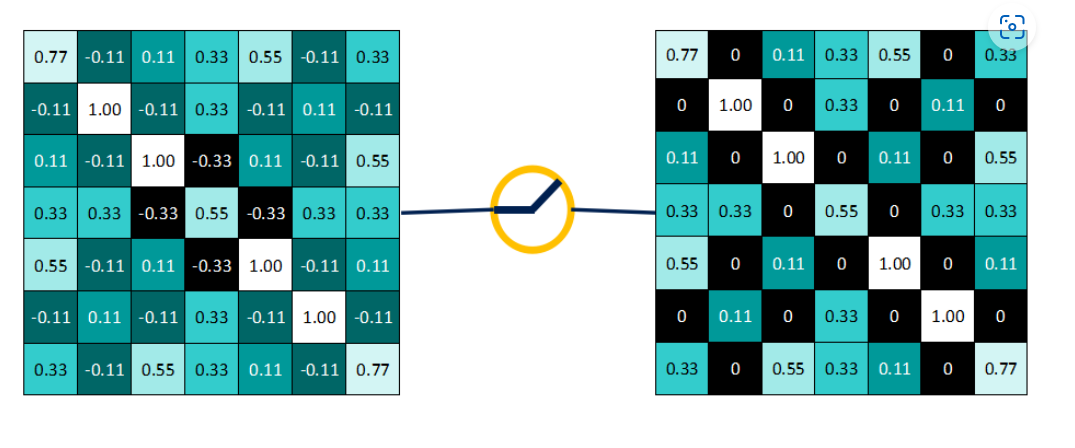
【池化层】pooling:减少数据量的方式,一般分为最大池化(Max pooling)和平均池化(Average pooling)两种
例如,选择池化尺寸为
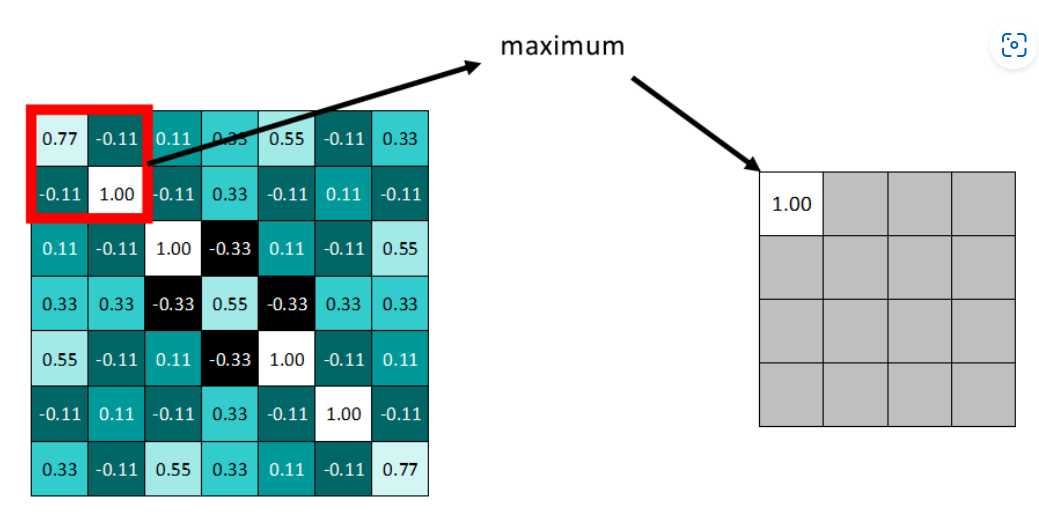
【全连接层】Fully-Connected / Linear:相邻层的所有节点全部连接
举例:
LeNet神经网络(数字识别)
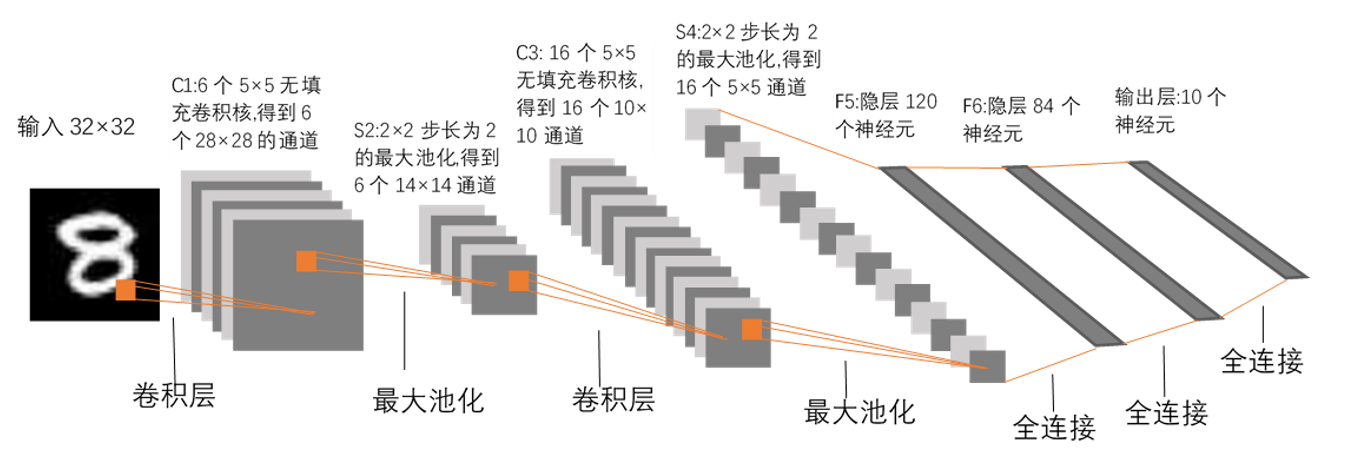
VGG-16神经网络(彩色图像)
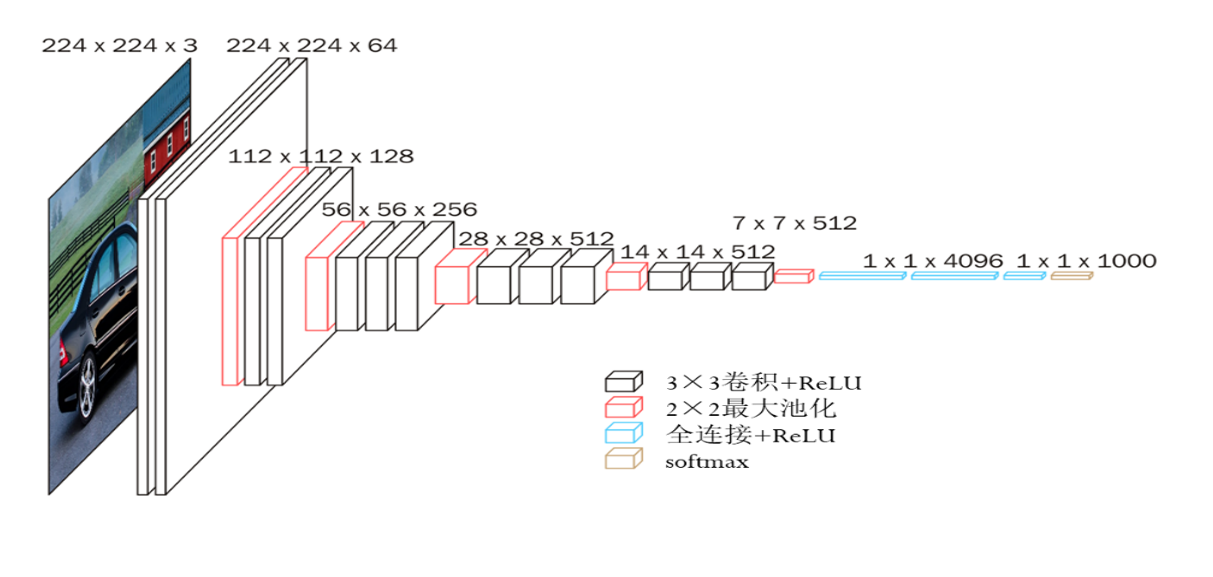
神经网络遇到的两大问题:① 梯度消失问题,② 过拟合问题
梯度消失问题:当神经网络层数增多之后,
比如说,
改进方式:
使用ReLU激活函数 此时,导数为1,而不是sigmoid的导数
GoogLeNet & Inception模块 分布输出,使得往下输入的梯度消失得到缓解: 损失函数同时考虑多个输出,求解多个输出的总和最小; 训练的时候多个输出一起输出,真正输出的时候只有一个
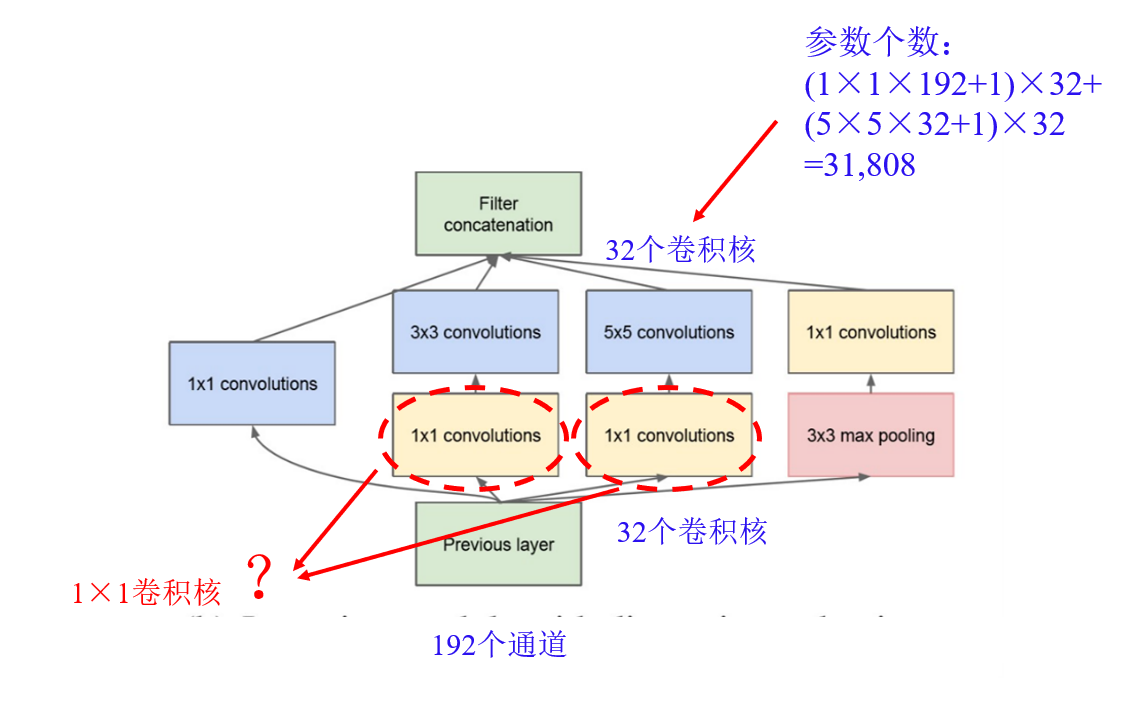
残差网络(ResNet) 起因:在讨论结构“K层神经网络 + 1层恒等映射”神经网络的退化现象(更深的网络在训练过程中的难度—— training error 和 test error 更大) 解决思路:将第“K+1层恒等映射”变为残差模块,按位相加
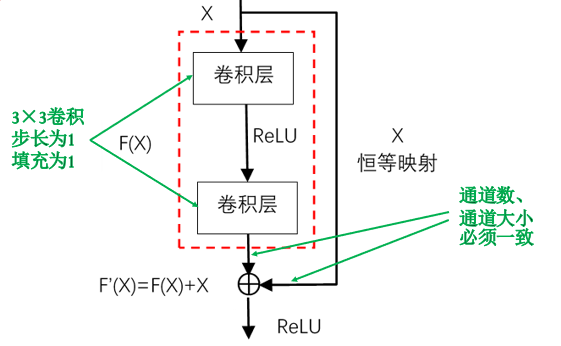
过拟合问题的解决方法
使用验证集:使用验证集确定迭代轮次停止点
正则化项法 在原误差平方和损失函数的基础上加入正则化项(以下以2-范数为例):
原理:降低模型复杂性(过拟合的很大概率源自于参数过大)
- 2-范数:很多参数值很小,但基本不会为0;抗干扰能力强
- 1-范数:一些参数为0,起到特征选择的作用
舍弃发(Dropout):每次训练随机地临时舍弃一些神经元
数据增强法:数据越多,过拟合的风险就越小 人为增加一些数据(例如图像的缩放、旋转、局部截取、改变颜色)
TextCNN:自然语言处理 NLP
1. 词向量
词向量的表示
独热(one-hot)编码:用与词表等长的向量表示一个词,向量只有一个元素为1(第
i个元素为1的向量用于表示此表中的第i个词),其余为0优点:编码简单,适用于稀疏向量 缺点:编码太长;无法度量词之间的相似性
分布式表示:可以度量词之间的相似性,适用于稠密向量
词嵌入 / Word embedding
每个词对应一个训练得到的词向量,是把词向量从高维空间嵌入到低维空间中的一个方法 语义相近的词,对应词向量的“距离”也越近
2. 语言模型 & 词向量的训练
用神经网络(NNLM / Neural Network Language Model)实现语言模型
模型结构:计算一个句子概率的模型 => 训练得到的词向量
Notation:
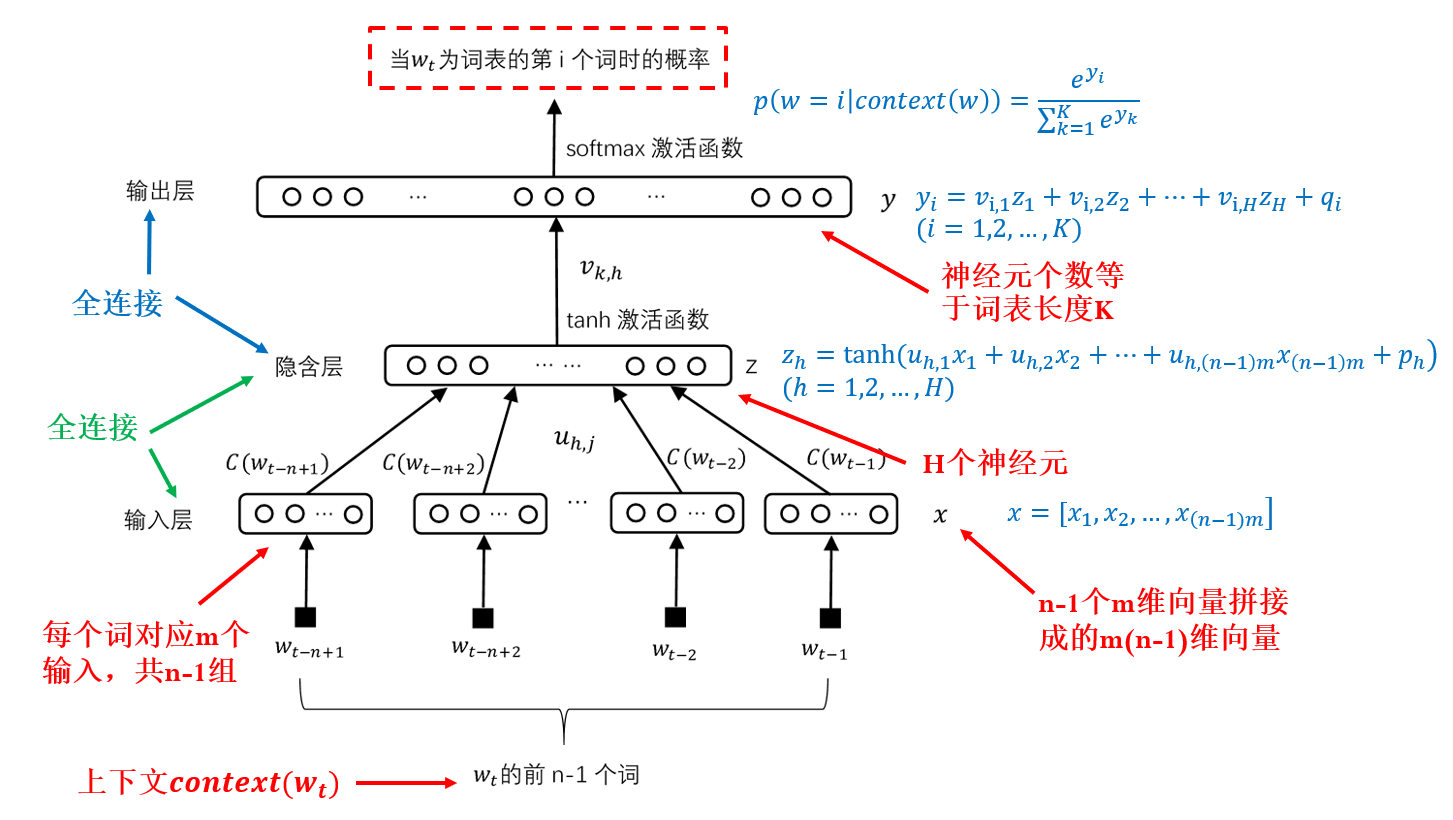
模型分析:实际上是用最大似然估计法在确定词向量(以及模型中的权重函数
举例:
假定语料库有
则联合概率:
希望上面的式子概率最大,得到
估计神经网络语言模型的参数:
表示:[给定神经网络参数
存在问题 输出层神经元个数等于词表长度
word2vec模型
一种简化的神经网络语言模型 两种实现方式:① 连续词袋模型(CBOW),② 跳词模型(Skip-Gram Model)
CBOW模型的特点:
① 词表的数字是连续的
② 词袋中不考虑词语的顺序(
下面详细介绍CBOW模型: Word2vec如何得到词向量-CSDN博客 CBOW模型的训练输入是某一个特征词的上下文相关的词对应的词向量(one-hot),而输出是一棵哈夫曼树。
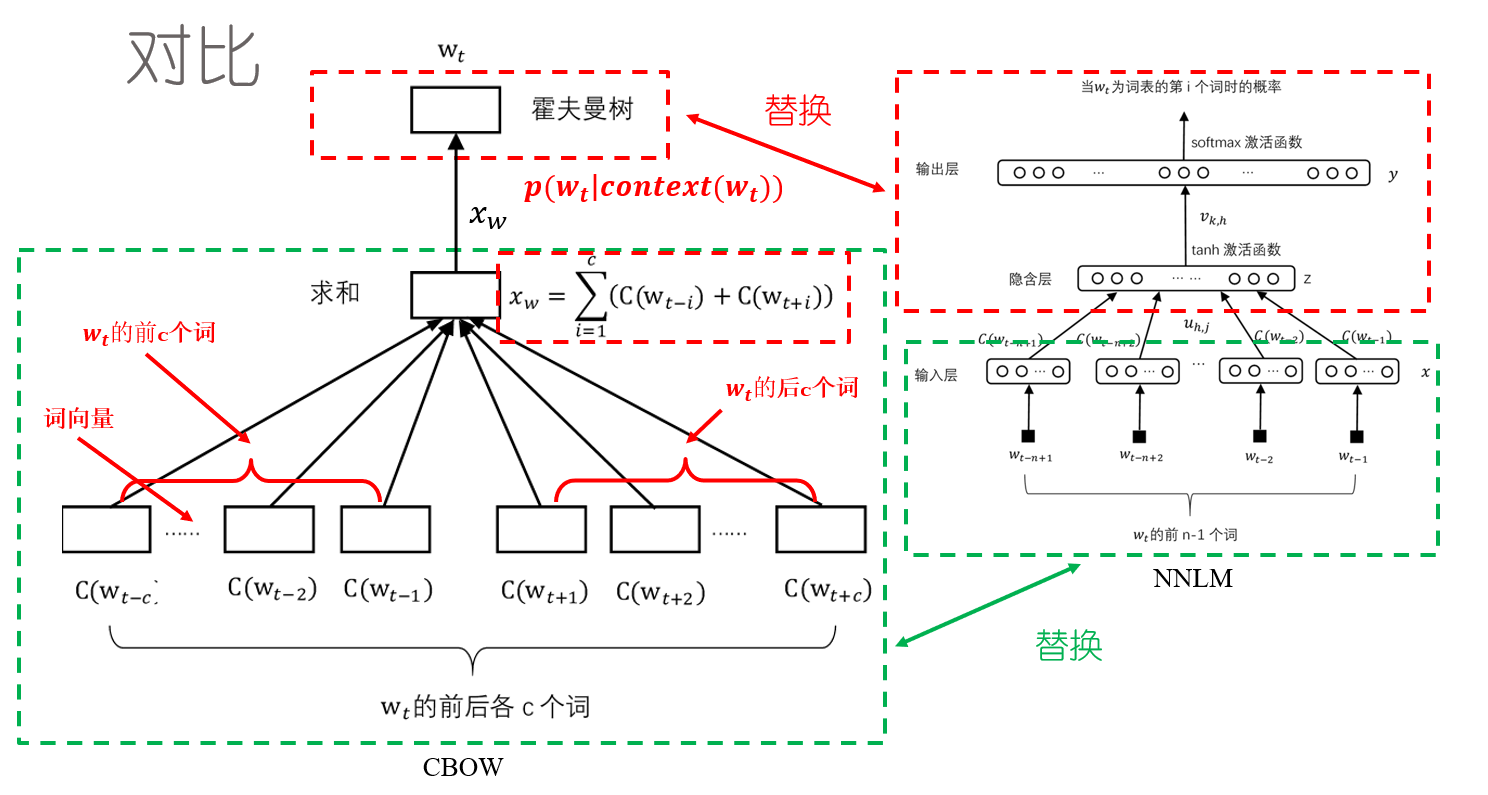
霍夫曼树与霍夫曼编码
词表内的词根据出现频率编码为霍夫曼树(左边为
1,右边为0)叶节点
非叶节点输入为
以
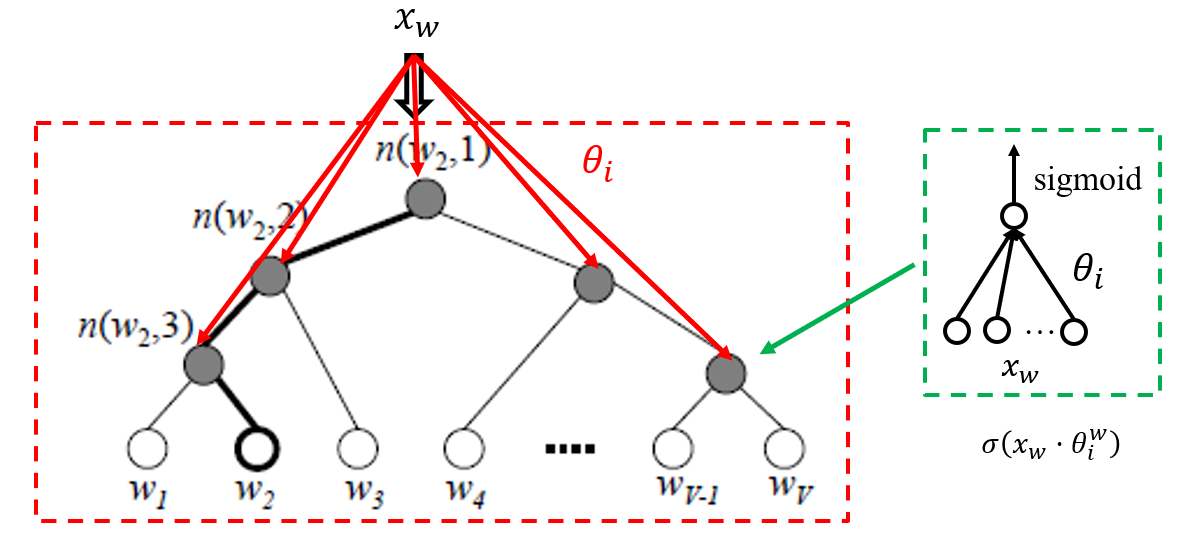
由此,可以定义词的最大似然函数以及损失函数(负对数函数),根据梯度上升(
优势:每次只计算与该词有关的参数;越是常用词涉及的参数越少
2.3 循环神经网络 RNN
RNN采用反馈网络机制,擅长处理序列数据(数据先后有所联系)
结构:全连接神经网络CNN的基础上增加上一时刻隐藏层反馈算法
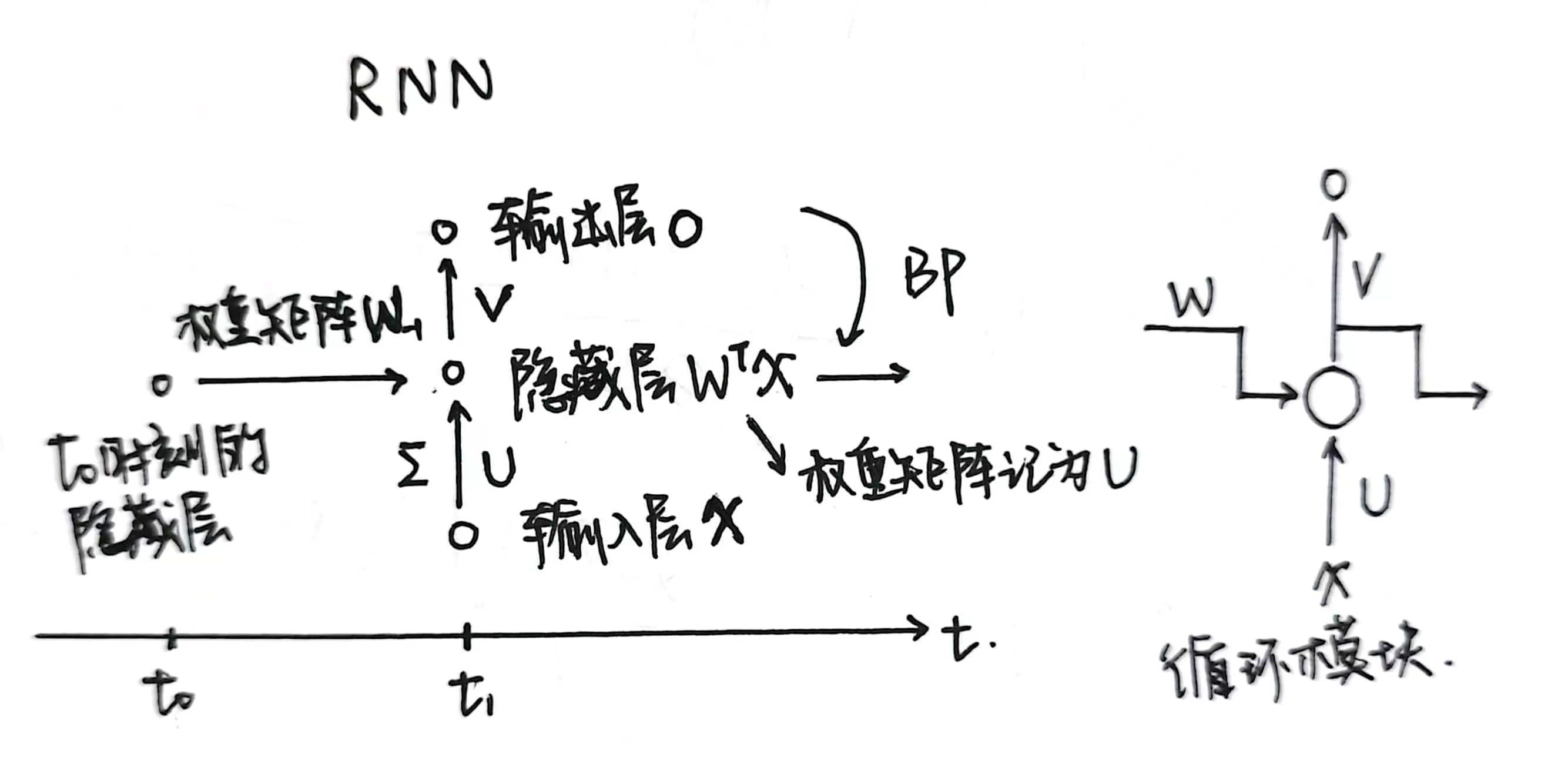
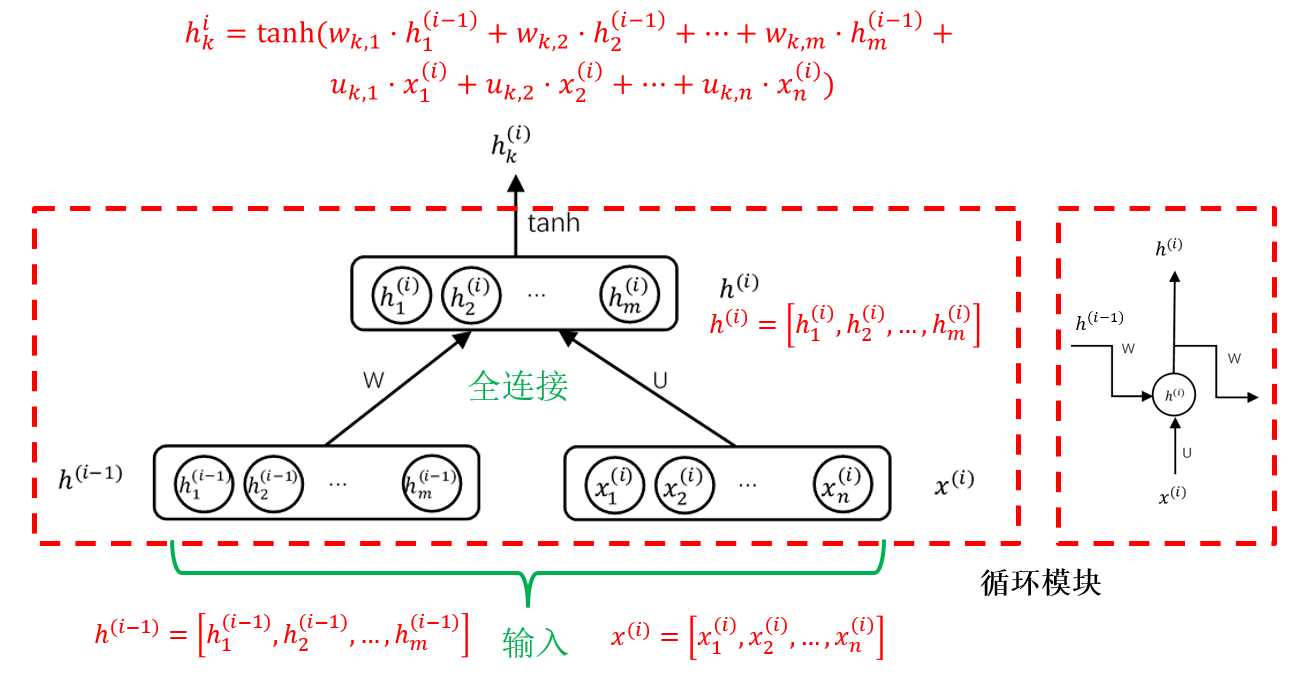
单向RNN存在的问题:序列前面的内容被后面的内容淹没
双向循环神经网络
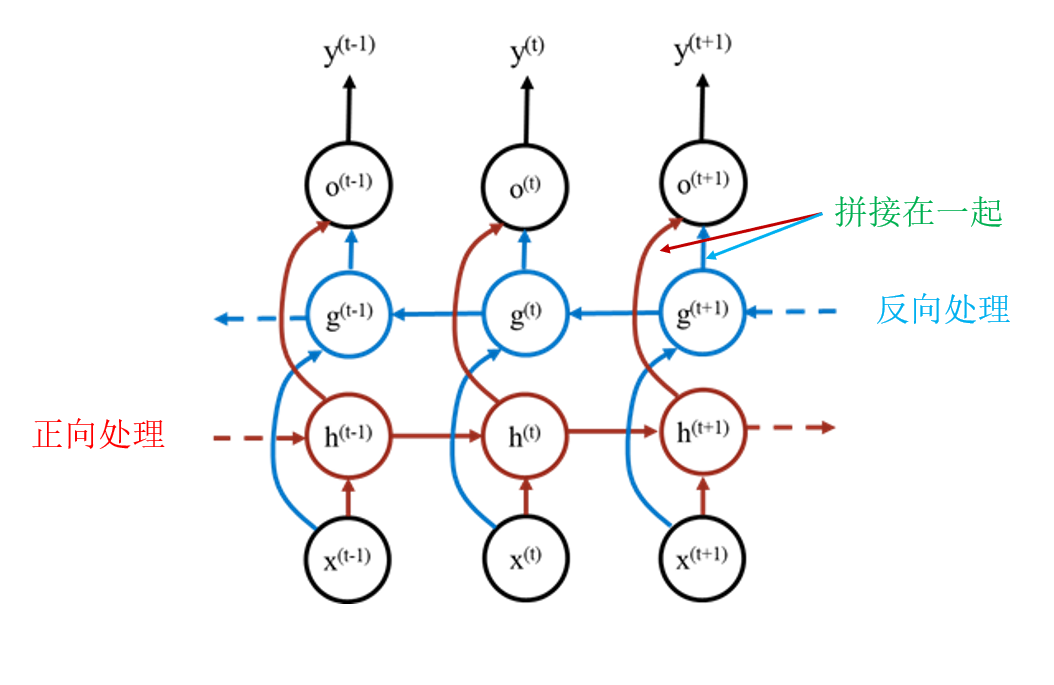
2.3.1 长短期记忆网络 LSTM
简单RNN存在的问题: ① 长期依赖问题(如:北京是一个美丽的(城市)vs 北京市一个美丽的(姑娘)) ② 重点选择问题(不同任务词的重要性不同)
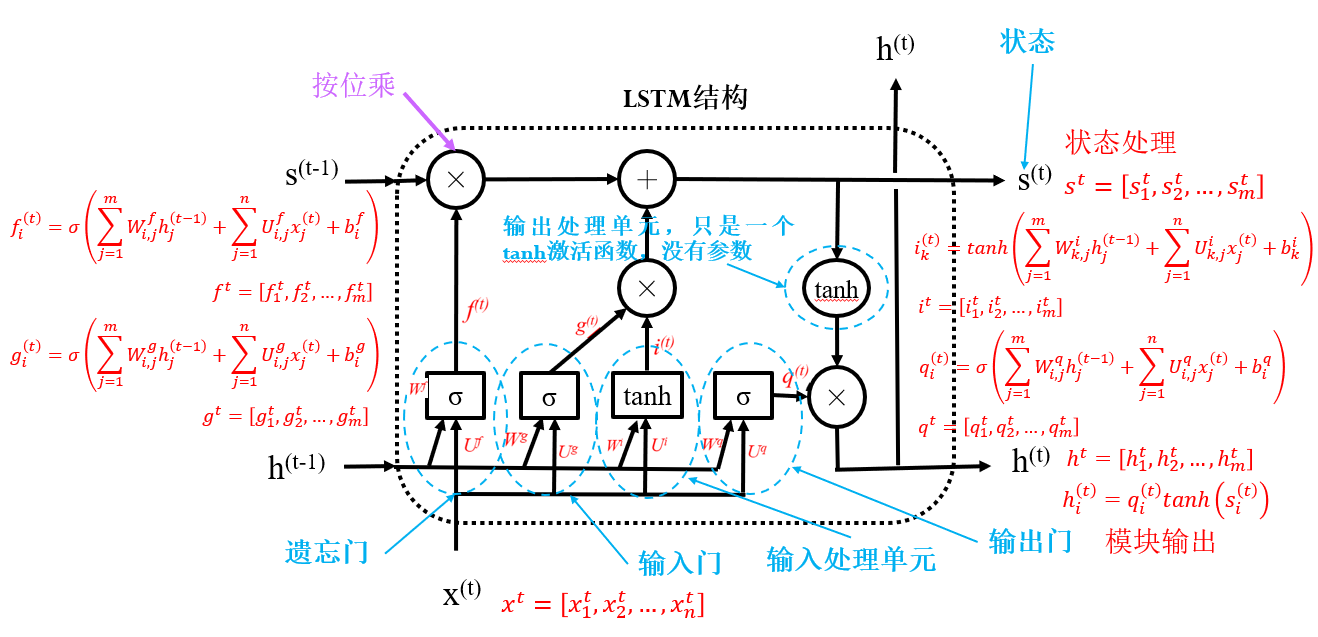
2.3.2 GRU
相比LSTM,使用GRU能够达到相当的效果,并且相比之下更容易进行训练,能够很大程度上提高训练效率
结构:LSTM的基础上,使用更少的门达到同样的处理效果
Chapter3 对抗搜索
博弈问题:双人 + 一人一步交替进行 + 双方信息完备 + 零和博弈 场景(极小-极大模型):A和B对抗博弈,一方A以评分(score)大为优,另一方B以评分小为优
3.1 α-β剪枝算法
极大节点[]的下界为α,极小节点()的上界为β
剪枝条件:(注意,这里的“祖先”不只包括“父节点”) 后辈节点的β值≤祖先节点的α值(极小≤极大)时,α剪枝 后辈节点的α值≥祖先节点的β值时(极大≥极小)时,β剪枝
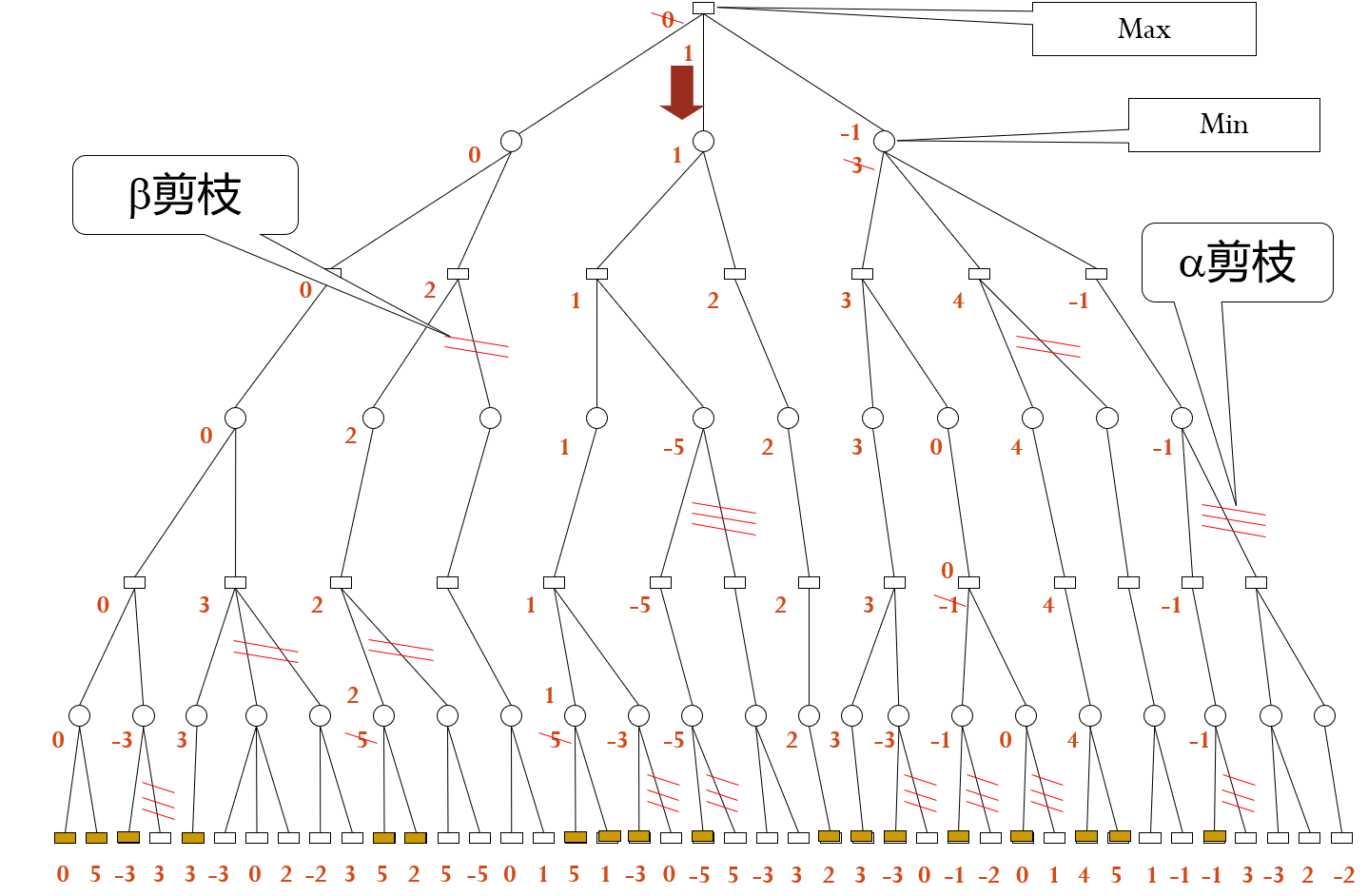
注意:一次剪枝过程只得到一次走步
方法问题:需要大量的专家知识
3.2 蒙特卡洛方法 MCM
蒙特卡洛方法(Monte Carlo methods)通过随机抽样、基于大数定律近似计算出问题的解或者评估问题的概率分布。即当样本量足够大时,样本的统计特征会趋近于总体的真实特征。
优势:应用于各种复杂的数值计算和概率统计问题,不需要事先对问题进行严格的数学推导,只需要进行大量的随机抽样和分析
劣势:计算效率通常较低,需要大量的计算资源和时间
接下来介绍蒙特卡洛树搜索 MCTS / Monte Carlo Tree Search:
.svg/808px-MCTS_(English).svg.png)
一种简介的理解方式:
步骤:选择(Select)
扩展(Expand) 模拟(Stimulate) 回溯(BackPropagate) 决策(Decide) 之后介绍课本上的MCTS步骤
蒙特卡洛树搜索通常包括以下三个阶段:
选择(Selection):从当前状态开始,根据一定的策略选择一个子节点进行扩展,即上述代码中的
不停的遍历、扩展节点
- 对于尚未完全被拓展的节点,随机选取未被扩展的子节点进行扩展(
expand()) - 对于完全被扩展的节点,选取最有希望的子节点(
bestChild())重复上述步骤
扩展(Expansion):对选定的子节点进行扩展,生成新的子节点
- 对于尚未完全被拓展的节点,随机选取未被扩展的子节点进行扩展(
模拟(Simulation):通过随机模拟的方式,在新生成的子节点上进行多次完整的随机模拟或者游戏对局,即上述代码中的
回溯(Backpropagation):根据模拟的结果,更新从根节点到当前节点路径上的统计信息,如胜率、访问次数等即上述代码中的
注意:更新的过程每一层都要“转换身份 / 正负号”!
决策(Decision):当到了一定的迭代次数或者时间之后结束,选择根节点下最好的子节点作为本次决策的结果,即上述代码中的
以上叙述中,“节点”表示某个需要决策的局面,或者当前状态(status)
UCT:“最有希望”的子节点用什么准则描述?
UCB算法(Upper Confidence Bound,信心上限算法):
UCT算法(Upper Confidence Bound Apply to Tree,上限置信区间算法):UCB算法 + MCTS算法
注意:UCT和上述MCTS的叙述不同——UCT中节点标注“获胜次数 / 模拟总次数”中的“获胜次数”是从本节点角度说的(下图中黑色节点代表己方状态,白色节点代表对手状态)
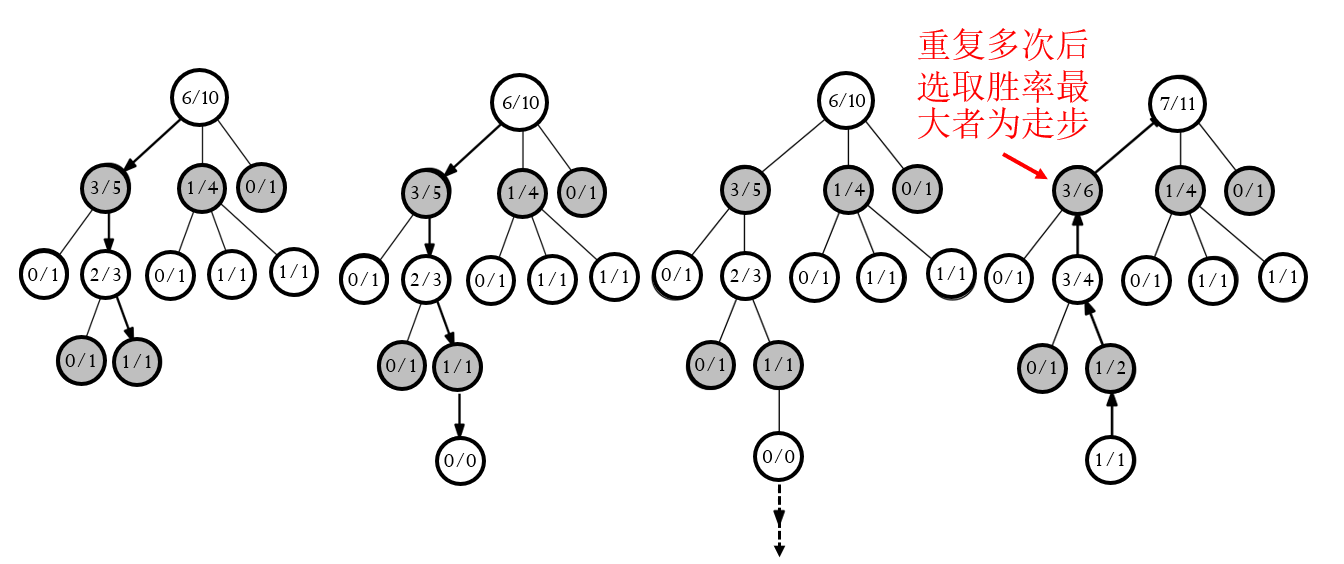
AlphaGo原理
待补充
3.3 深度强化学习方法(围棋)
强化学习:学习“做什么才能使得收益最大化”的方法;学习者不会被告知如何做,必须自己通过尝试发现哪些动作会产生最大的收益 特征:试错和延迟收益(区别于监督学习)
深度强化学习:用深度学习(神经网络)实现的强化学习;关键在于损失函数的定义 三种实现方式:基于策略梯度的强化学习、基于价值评估的强化学习、基于演员-评价方法的强化学习
基于策略梯度的强化学习:学习到的是每个落子点获胜的概率
数据:自我博弈产生,
Notations:
损失函数:
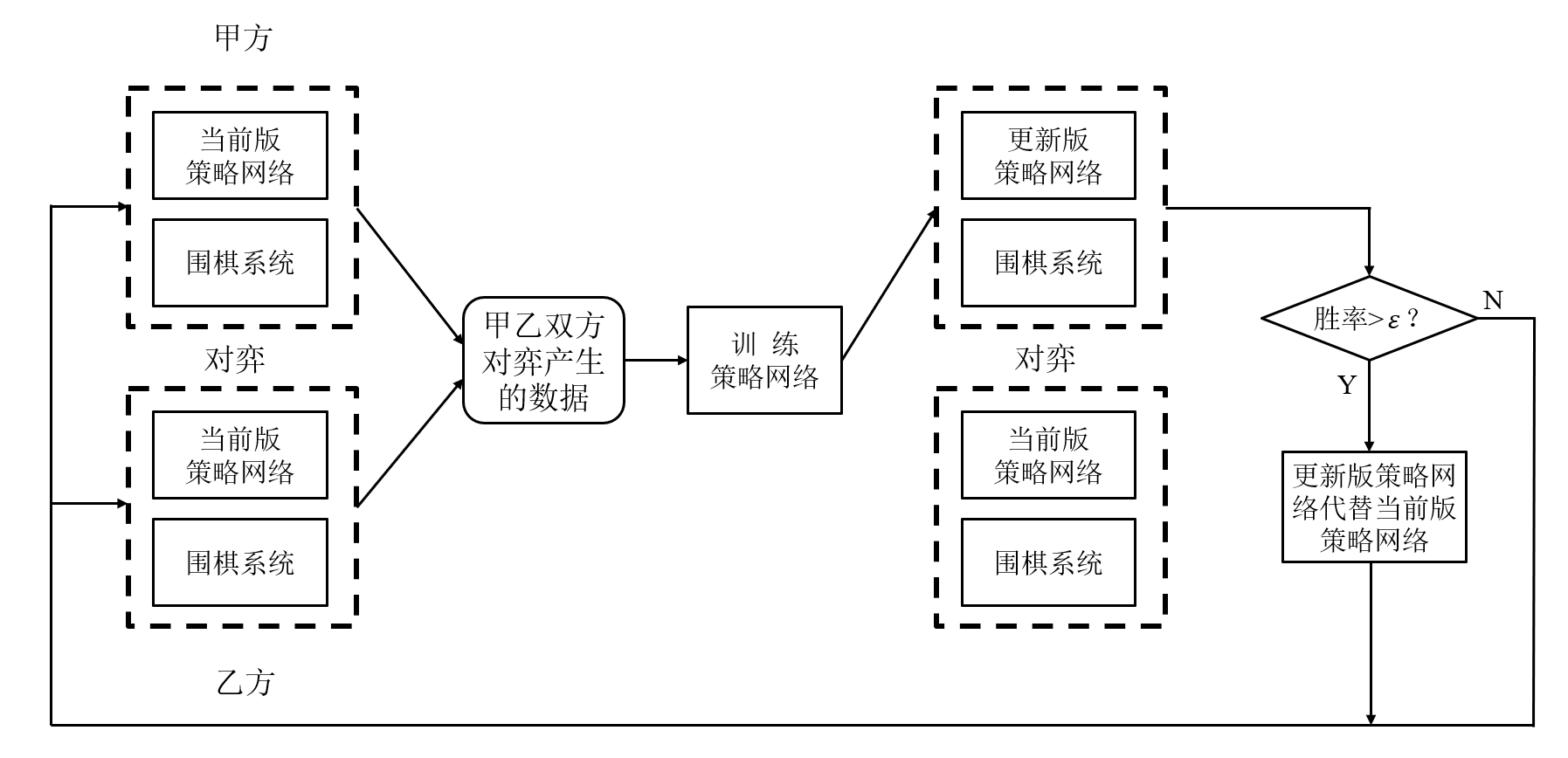
注意:
- 在强化学习过程中,每个样本只使用一次
- 基于策略梯度的强化学习方法学到的是在每个可落子点行棋的获胜概率(监督学习策略网络学到的是在某个可落子点行棋的概率)
基于价值评估的强化学习:学习到的是每个落子点获取最大收益的概率
对一个行棋点的价值,也就是收益进行评估
- 输入:当前棋局和行棋点
- 输出:取值在[-1,1]之间的估值
数据:自我博弈产生,
Notations:
损失函数:
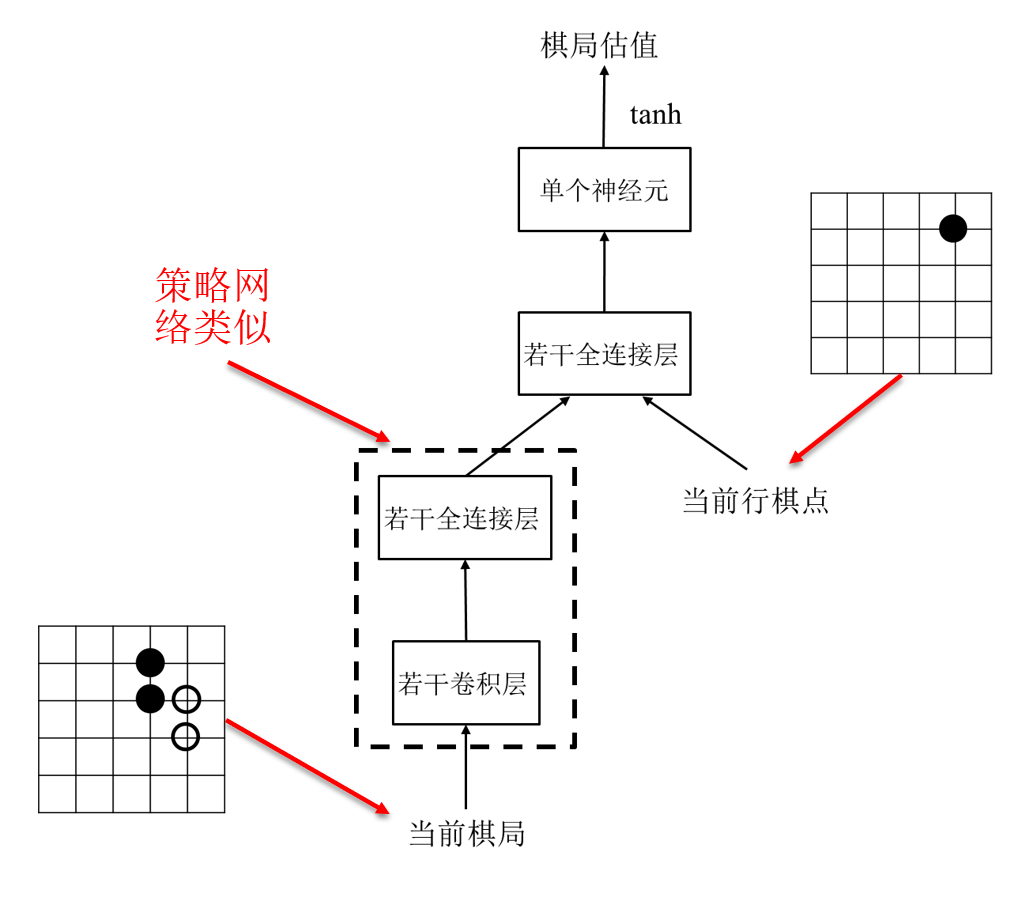
基于演员-评价方法的强化学习:学习到的是每个落子点获得最大收益增量的概率
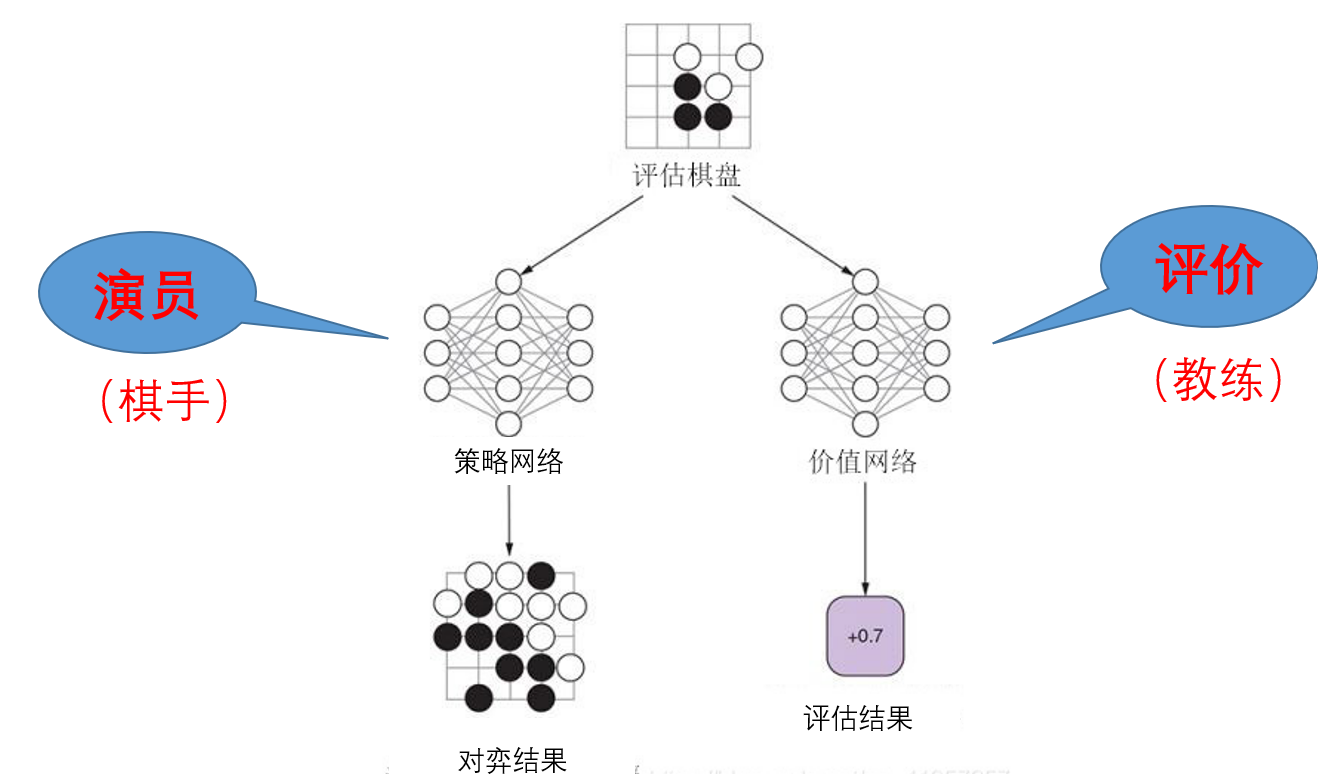
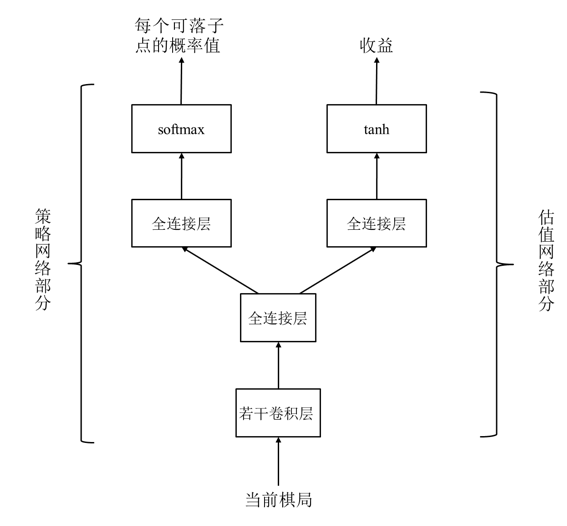
收益增量评价一步棋的好坏:
Notations:
损失函数:
- 评价部分:
- 演员部分:
获胜概率 - 综合损失函数:
- 评价部分:
AlphaGo Zero 强化学习
待补充
Chapter4 统计机器学习
统计机器学习方法:学习算法
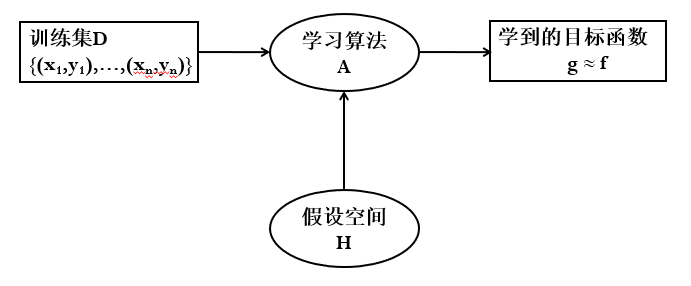
三要素:模型、策略、算法 模型:学习什么样的模型(条件概率分布、决策函数) 策略:模型选择的准则(经验风险最小化、结构风险最小化) 算法:模型学习的算法(一般归结为一个最优化问题)
4.1 支撑向量机 SVM
SVM:Support Vector Machines,是一个二分类器——特征空间上的间隔最大化线性分类器,通过核技巧可以实现非线性分类
函数间隔:
几何间隔:
最优分界面:即间隔最大的超平面,满足
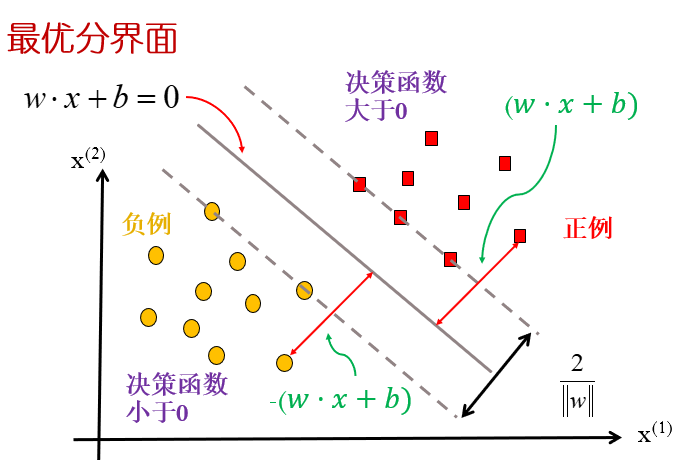
由于函数间隔是可缩放的,成比例变化不影响最优化问题,所以可取
转化为如下的凸二次规划问题:
1. SVM与对偶算法
原始问题:
定义拉格朗日函数:
拉格朗日函数与原始优化问题的关系:
求解对偶问题:对
利用KKT条件,得到:
其中,
例题:

2. “线性不可分”支持向量机
某些点线性不可分,意味着这些点不满足函数间隔大于等于
称为软间隔最大化。其中
此时,Lagrange对偶函数为:
求解思路同前,但是
其中,
- 若
- 若
- 若
- 若
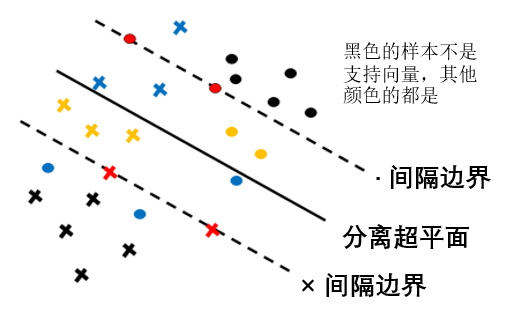
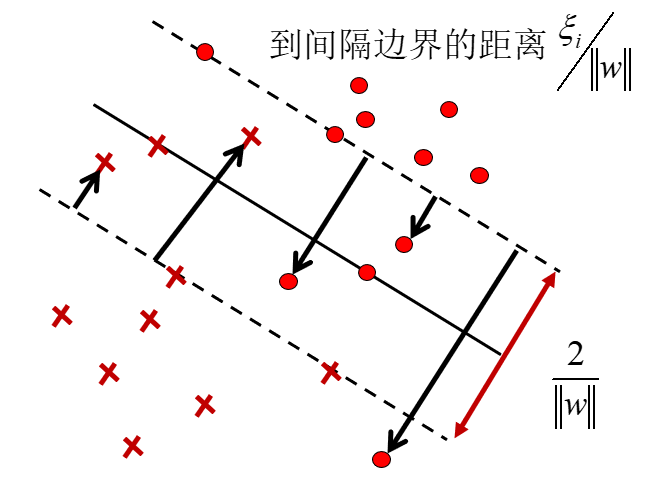
线性可分时,最大间隔是取函数间隔为
注意:即使是线性可分问题,如果
3. 非线性支持向量机
设变换:
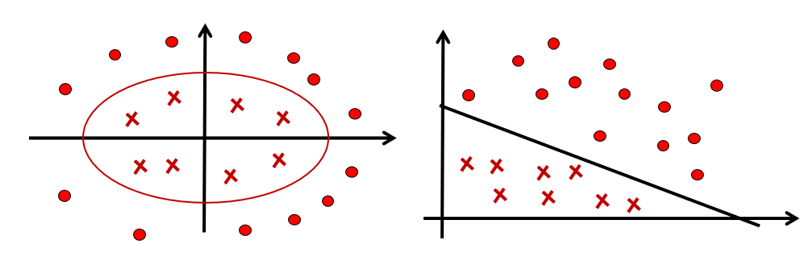
核技巧:通过一个非线性变换将输入空间X(欧式空间或者离散集合)对应于一个特征空间H(希尔伯特空间),使得在输入空间X的超曲面模型对应于特征空间H中的超平面模型(支持向量机)。分类问题的学习就可以通过在H空间中求解线性支持向量机完成。
非线性支持向量机的对偶问题:
核函数:设
使得对所有
则称
因此,非线性支持向量机的对偶问题化简为:
正定核的充要条件
设
常用的核函数
- 多项式核函数:
- 高斯核函数:
- 多项式核函数:
序列最小最优化算法 SMO / Sequential Minimal Optimization 抽象来说,每次取两个
SVM用于求解多分类问题:
- 一对多:某类为正例,其余为负例;分类时将未知样本分类为具有最大分类函数值的那类(共构造
- 一对一:任意两类构造一个SVM(共构造
- 层次法:所有类先分成两类
文本分类的特征抽取
文本表达为一个向量:
- 词频
- 词频
4.2 决策树
给定训练集:
决策树学习就是从训练集中归纳出一组分类规则,得到一个与训练集矛盾较小的决策树的过程——是一个NPC问题,所以一般采用启发式方法得到一个近似解(损失函数最小作为优化目标)
特征选择:用信息增益选择特征
随机变量
条件熵:
特征
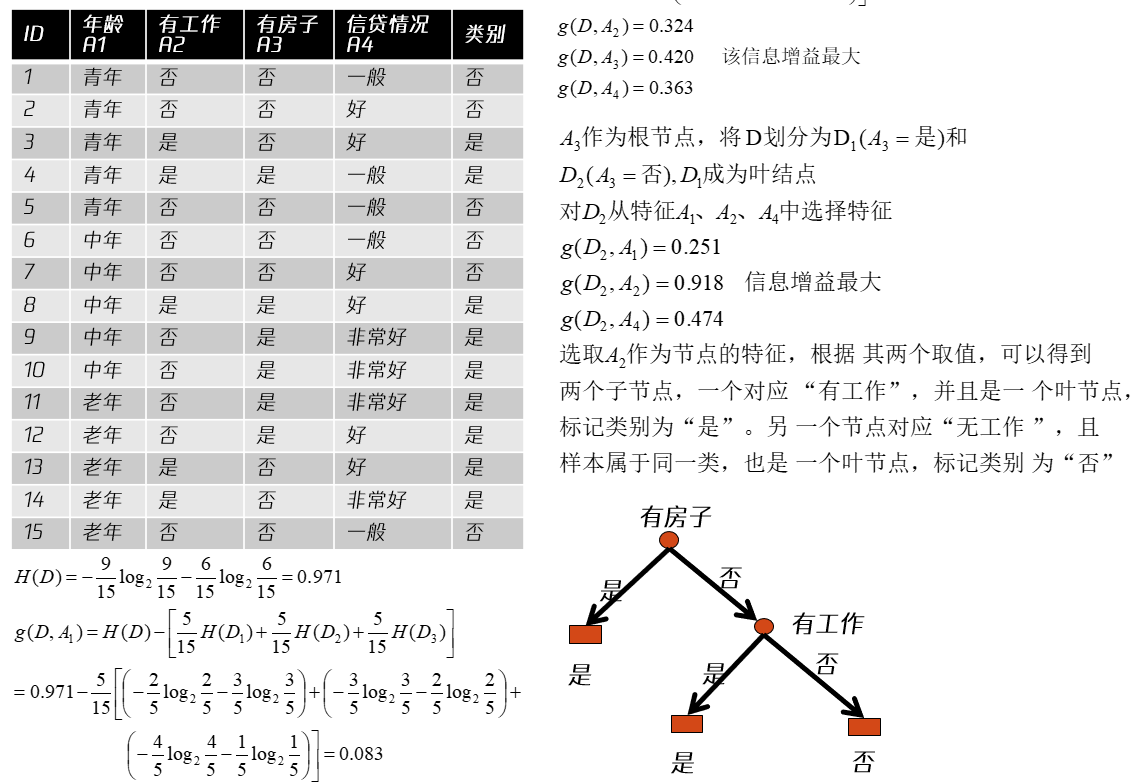
举例:设训练集
1. ID3算法
选择一个最大信息增益的特征,如果它足够好(信息增益比较大),那么就按这个特征先分一次类,然后递归建树即可
输入:训练集
输出:决策树
- 若
- 若
- 否则计算
- 如果
- 否则,对
- 对于
- 否则,以
存在的问题:倾向于选择分支比较多的属性
2. C4.5算法
信息增益比:
C4.5增加了对连续值属性的处理,对于连续值属性
存在的问题:倾向于选择分割不均匀的特征
解决办法:先选择
后来发展到了C5.0
3. 决策树的剪枝
后剪枝(先生成树再剪枝):为了防止出现过拟合,从已经生成的树上裁掉一些子树或者叶节点,将其父节点作为新的叶节点,用其实例数最大的类别作为标记。
当数据量小时,直接利用训练集进行剪枝
从下向上逐步剪枝;再验证集上测试性能,直到性能下降位置
剪枝的数学模型:当
通俗理解:每个节点的经验熵
4. 随机森林
随机森林是由多个决策树组成的分类器;通过投票机制改善决策树 单个决策树的生成:有放回的数据采样,属性(特征)的采样 集外数据的使用:单个决策树的未用到的数据