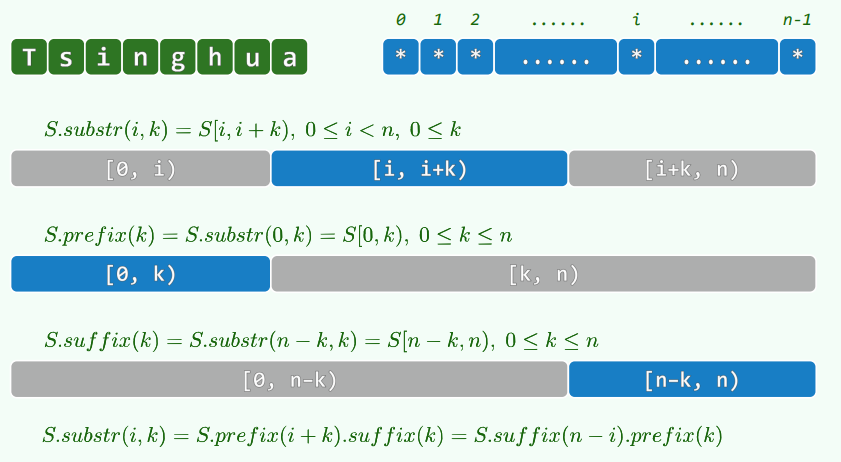
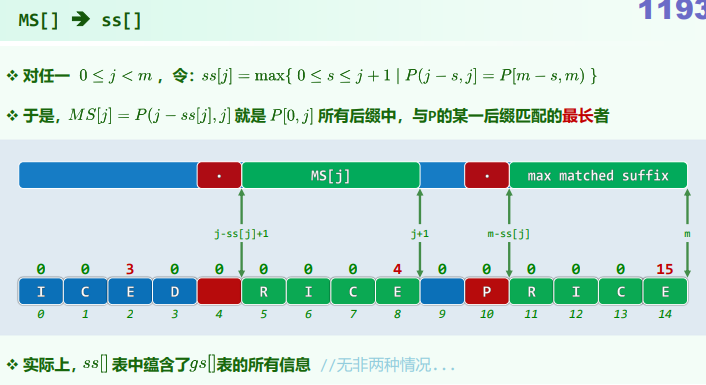
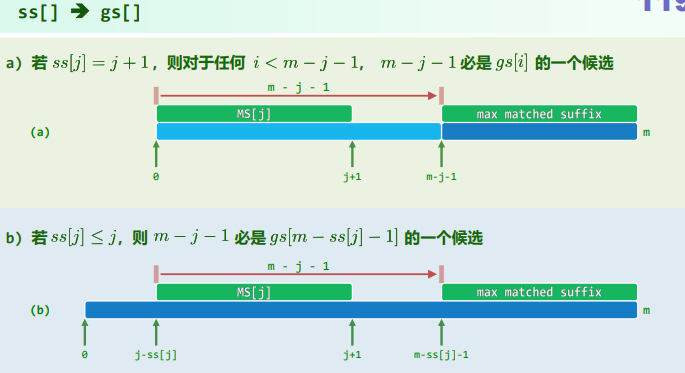
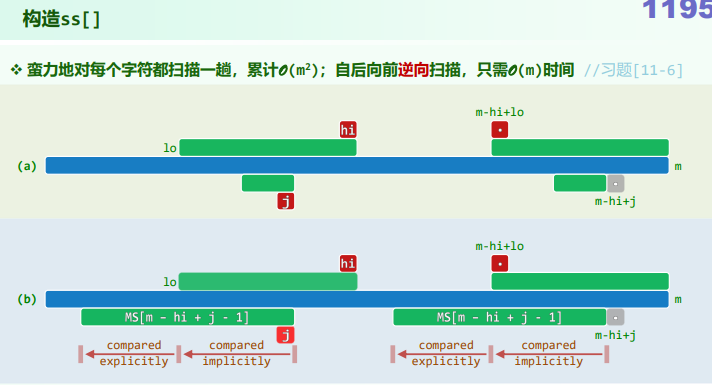
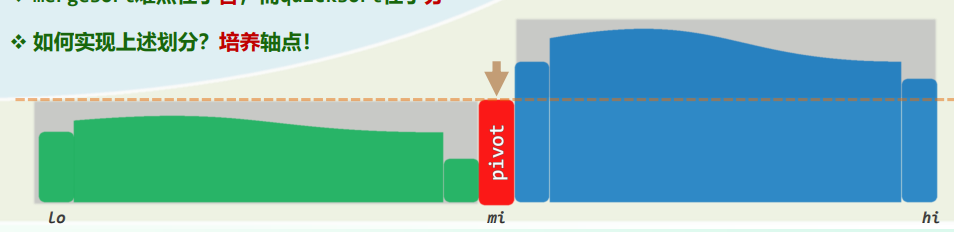
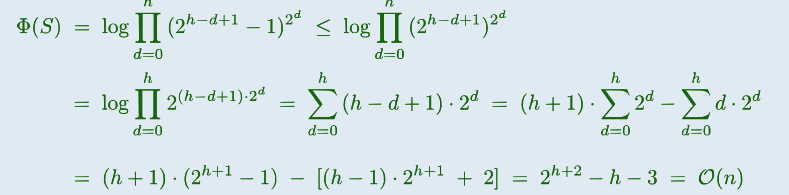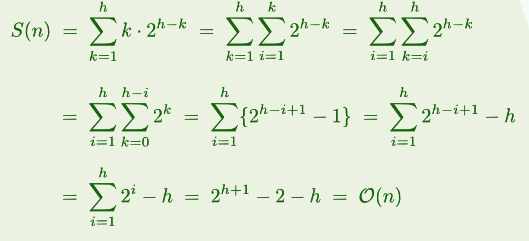数据结构
Author: 经12-计18 张诗颖 2021011056
1 绪论
1. 工具:尺规计算机
2. 算法
要求:正确性、确定性、可行性、有穷性
好算法:正确、健壮、可读、效率
正确性证明:Loop Invariant, Convergence, Correctness
[EG/有穷性]:Hailstone序列(尚未证明或证否)
while (1 < n) { n % 2 ? n = 3 * n + 1 : n / 2; length++;}3. 计算模型
图灵机 (Turing Machine)

- Tape:依次均匀地划分为单元格,各存有某一字符(初始为
#),理想假设无限长 - Head:总是对准某一单元格,可读写;经过一个节拍可转向左右邻格
- Alphabet:字符的种类有限
- State:图灵机总是处于有限种状态中的某一种,约定
'h' = halt
Transition Function:
(q, c; d, L/R, p)(当前状态q,当前字符c,改写d,状态p) [EG]:(<, 1; 0, L, <)计算成本:从启动至停机所经历的节拍数目/Head累计的移动次数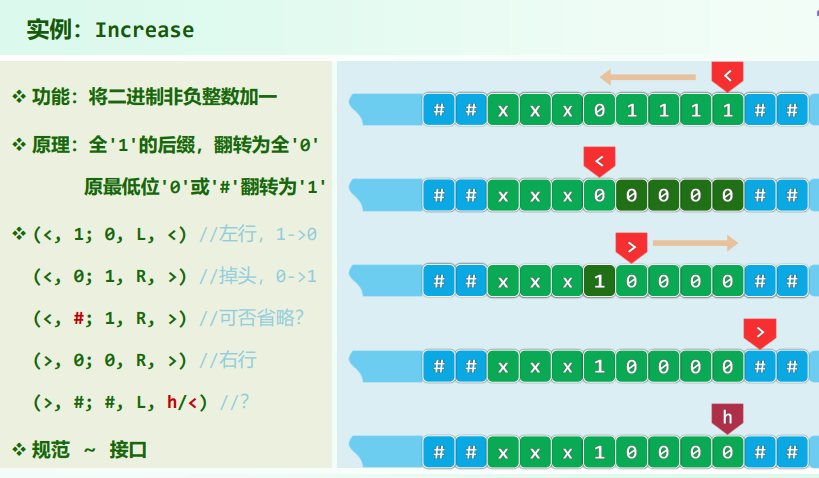
- Tape:依次均匀地划分为单元格,各存有某一字符(初始为
RAM (Random Access Machine)
寄存器顺序编号,总数没有限制
可通过编号直接访问任意寄存器 call-by-rank
每一基本操作(10个)仅需常数时间
xxxxxxxxxxR[i] <= c R[i] <= R[R[j]] R[i] <= R[j] + R[k]R[i] <= R[j] R[R[i]] <= R[j] R[i] <= R[j] - R[k]IF R[i] = 0 GOTO # IF R[i] > 0 GOTO #GOTO # STOP
计算成本:算法需要执行的基本操作次数
[EG]:Ceiling Division(除法上整)
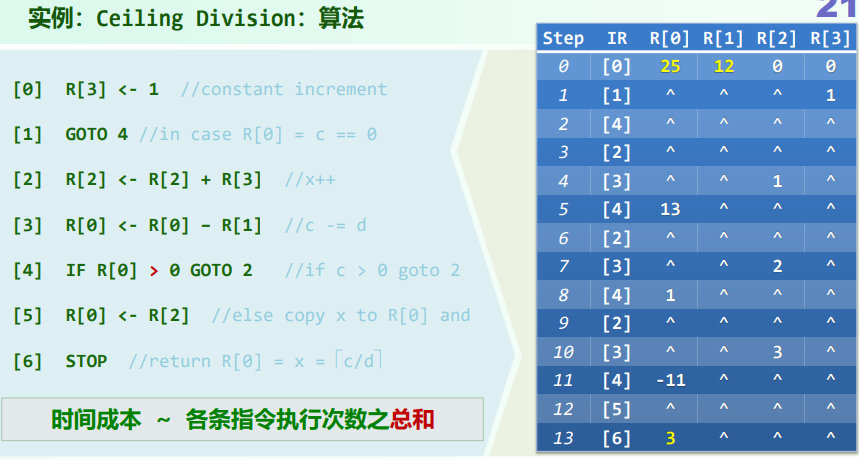
1.1 渐进复杂度:大O记号
Paul Bachmann, 1894: T(n) = O(f(n)) iff
c > 0 s.t. T(n) < c · f(n) n >> 2 T(n) = (f(n)) iff c > 0 s.t. T(n) > c · f(n) n >> 2 T(n) = (f(n)) iff c1 > c2 > 0 s.t. c1· f(n) > T(n) > c2· f(n) n >> 2
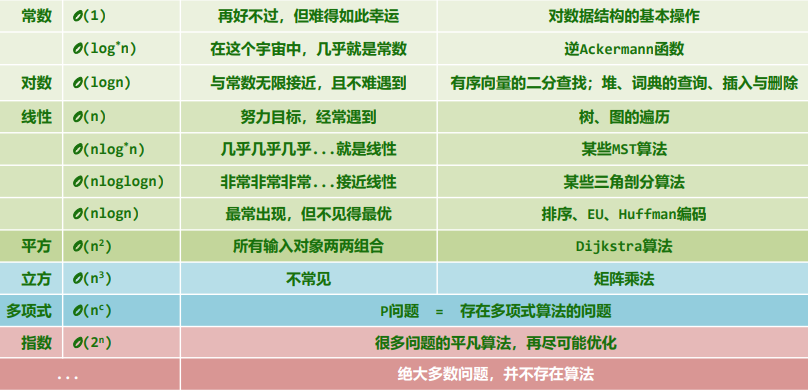
O(1):constant
O(logcn):poly-log,复杂度无限接近于常数(
NP = Non-deterministic Polynomial
1. 级数复杂度
算术级数:与末项平方同阶
幂方级数:比幂次高出一阶
几何级数:与末项同阶

几何分布(收敛级数):O(1)
不收敛级数 调和级数 (
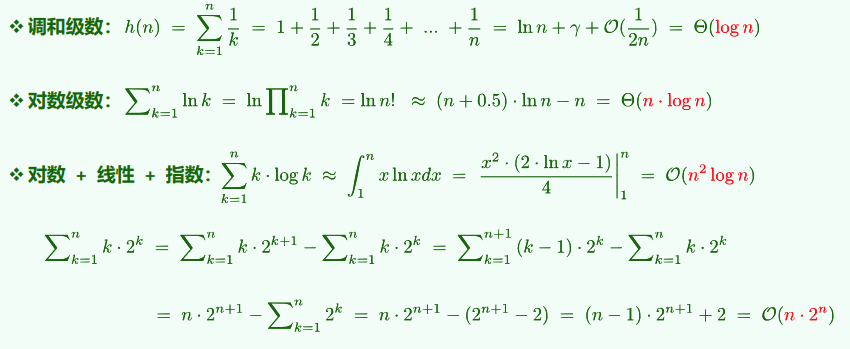
2. 复杂度分析
- 常见的二层循环
xfor (int i = 0; i < n; ++i) for (int j = 0; j < n; ++j) // 把n改成i,++j改成j+=const => 复杂度不变 for (int i = 1; i < n; i <<= 1) for (int j = 0; j < i; ++j)
for (int i = 0; i <= n; ++i) for (int j = 1; j < i; j += j)封底估算:Back-Of-The-Envelope Calculation
1 day ≈ 105 sec 1生 ≈ 1 世纪 ≈ 3 × 109 sec 三生三世 ≈ 300yr ≈ 1010 sec 宇宙大爆炸至今 ≈ 4 × 1017 sec
普通PC:1GHz,109 flops 天河1A:1P,1015 flops

任何算法其时间复杂度一般是空间复杂度的上界(所以一般不首先考虑空间复杂度)
1.2 迭代与递归
递归跟踪:绘出计算过程中出现过的所有递归实例及其调用关系,他们各自所需时间之和为整体运行时间
递推方程:[EG/Sum] T(n) = T(n - 1) + O(1), base: T(0) = O(1) => 求解
1. 减而治之
Decrease-and-conquer,将原问题划分为两个子问题,一个平凡,一个规模缩减 递归的潜在问题:空间复杂度爆炸
[EG/Reverse]:
递归版:
xxxxxxxxxxif (low < high) { swap(A[low], A[high]); reverse(A, low + 1, high - 1);}迭代版:
xxxxxxxxxxwhile (low < high) swap(A[low++], A[high--])2. 分而治之
Divide-and-conquer,将原问题划分为若干个子问题,且子问题规模大体相当
[EG/BinaryRecursion]:
xxxxxxxxxxsum(int A[], int lo, int hi) { //[lo, hi) if (hi - lo < 2) return A[lo]; int mi = (hi + lo) >> 1; return sum(A, lo, mi) + sum(A, mi, hi)}3. Master Theorem
分治策略对应的递推式通常形如:T(n) = a·T(n/b) + O(f(n))
[解释]:原问题被划分为a个规模均为n/b的子任务;任务的划分,解的合并耗时f(n)
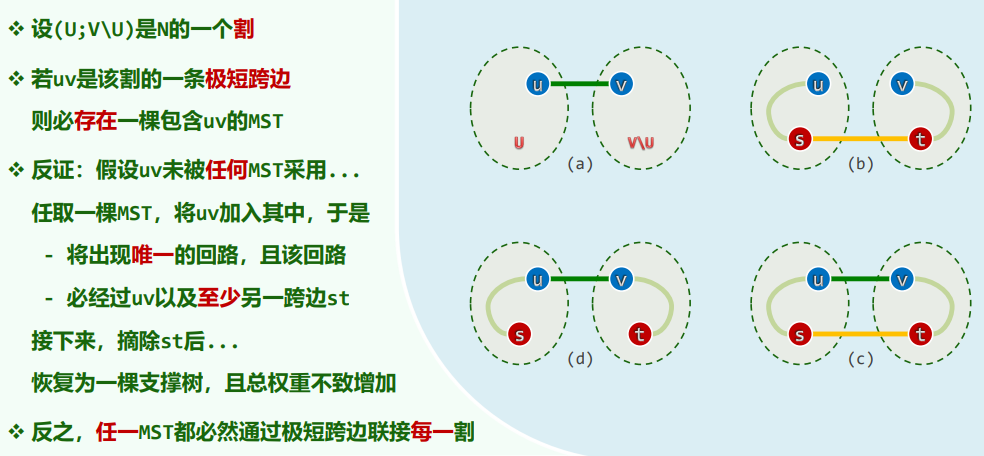
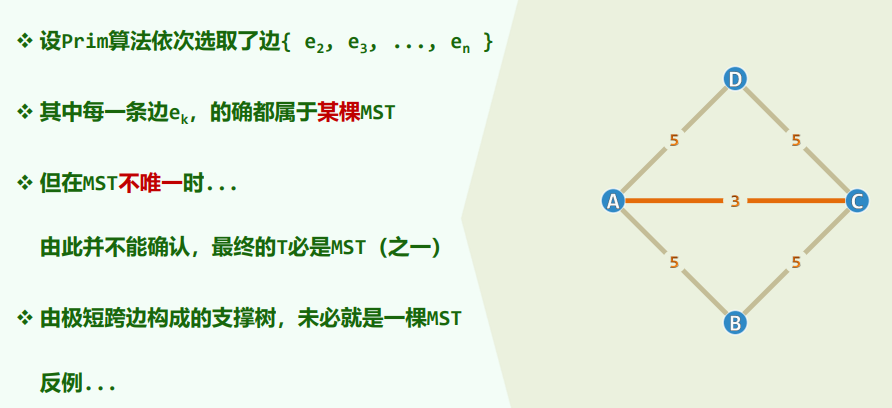
- 若
T(n) = 2·T(n/4) + O(1) = O(n^(1/2)) - 若
T(n) = 1·T(n/2) + O(1) = O(logn)[EP/mergesort]:T(n) = 2·T(n/2) + O(n) = O(nlogn)[EP/STL-mergesort]:T(n) = 2·T(n/2) + O(nlogn) = O(nlog^2n) - 若
T(n) = 1·T(n/2) + O(n) = O(n)
4. EP:Multiplication
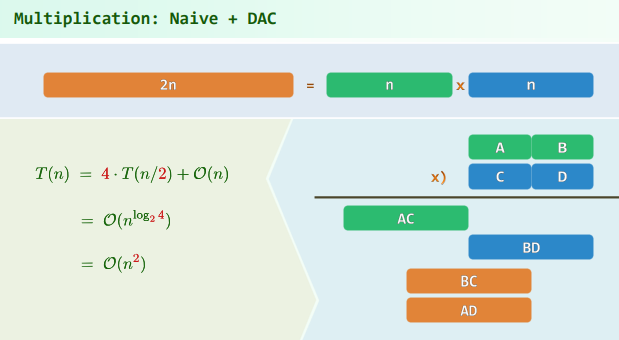
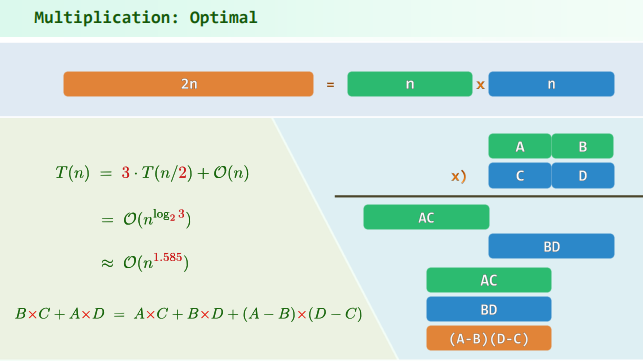
5. EP:总和最大区段
问题描述:从整数序列中,找出总和最大的区段(有多个时,短者优先)
蛮力算法:O(n3)
xxxxxxxxxxint gs_BF(int A[], int n) { //Brute Forceint gs = A[0]; //当前已知的最大和for (int i = 0; i < n; ++i)for (int j = i; j < n; ++j) { //枚举所有O(n^2)个区段int s = 0;for (int k = i; k <= j; ++k) s += A[k]; //用O(n)时间求和if (gs < s) gs = s; //择优,更新}return gs;}递增策略:O(n2)
xxxxxxxxxxint gs_IC(int A[], int n) { //Incremental Strategyint gs = A[0]; //当前已知的最大和for (int i = 0; i < n; ++i) { //枚举所有起始于iint s = 0;for (int j = i; j < n; ++j) { //终止于j的区间s += A[j]; //递增地得到其总和:O(1)if (gs < s) gs = s; //择优,更新}}return gs;}分治策略:O(nlogn)
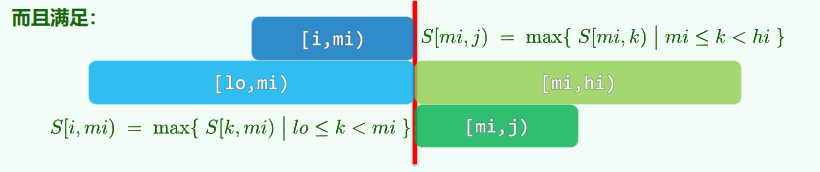
xxxxxxxxxxint gs_DC(int A[], int lo, int hi) { //Divide-and-Conquerif (hi - lo < 2) return A[lo]; //递归基int mi = (lo + hi) / 2;int gsL = A[mi - 1], sL = 0, i = mi; //枚举while (lo < i--) //所有[i, mi)类区段if (gsL < (sL += A[i])) gsL = sL;int gsR = A[mi], sR = 0, j = mi - 1; //枚举while (++j < hi) //所有[mi, j)类区段if (gsR < (sR += A[j])) gsR = sR; //更新return max(gsL+ gsR, max(gs_DC(A, lo, mi), gs_DC(A, mi, hi)));}减治策略:O(n) 构思:考察最短的总和非正的后缀A[k, hi),以及总和最大的区段GS(lo, hi) = A[i, j),可以发现后者要么是前者的(真)后缀,要么与前者无交。
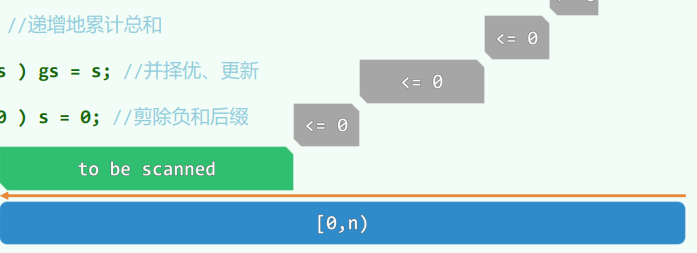
xxxxxxxxxxint gs_LS(int A[], int n) { //Linear Scanint gs = A[0], s = 0, i = n;while (0 < i--) { //在当前区间内s += A[i];if (gs < s) gs = s; //择优,更新if (s <= 0) s = 0; //剪除负和后缀}return gs;}
1.3 动态规划
动态规划:Dynamic Programming,一种颠倒计算方法,自底而上迭代的方式。
[EG/fibonacci]:T(n) = O(n)
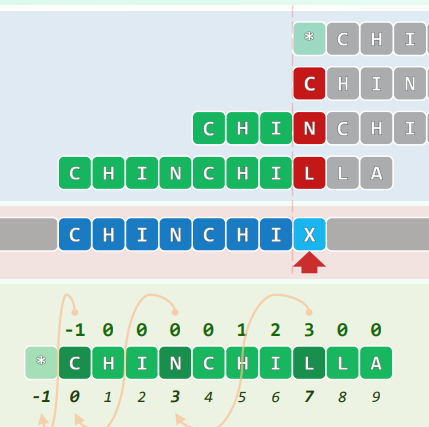
xxxxxxxxxxf = 1; g = 0;while (0 < n--) { g = g + f; f = g - f;}return g;1. EP:最长公共子序列
减而治之——递归:复杂度
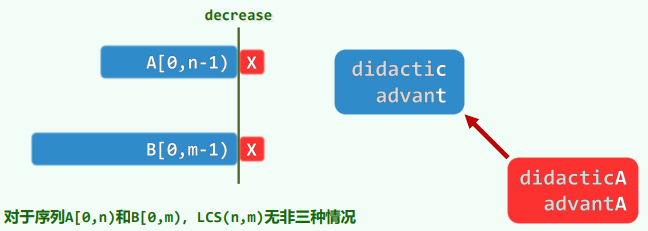
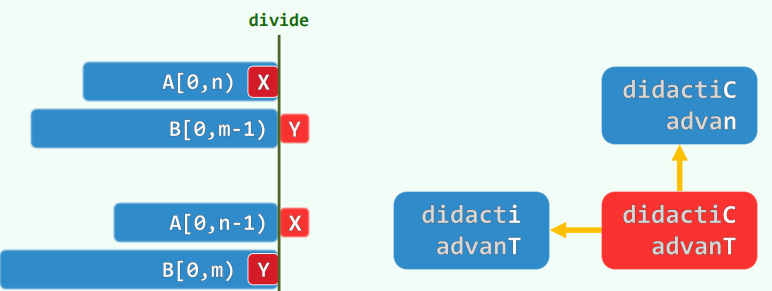
递归基:
n = 0或m = 0取作空序列""(长度为零) 若A[n - 1] = 'X' = B[m - 1],则取作:LCS(n - 1, m - 2) + 'X'若A[n - 1] ≠ B[m - 1],则在LCS(n, m - 1)与LCS(n - 1, m)中取更长者动态规划——递推:复杂度
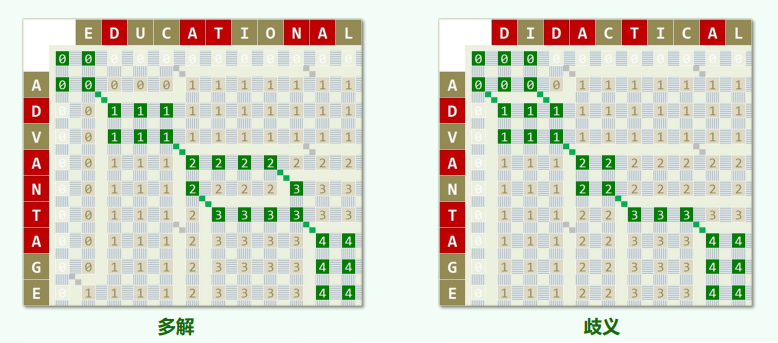
xxxxxxxxxxunsigned int lcs(char const * A, int n, char const * B, int m) {if (n < m) { //make sure m <= nswap(A, B);swap(n, m);}unsigned int* lcs1 = new unsigned int[m + 1]; //the current two rows areunsigned int* lcs2 = new unsigned int[m + 1]; //buffered alternativelymemset(lcs1, 0x00, sizeof(unsigned int) * (m + 1));memset(lcs2, 0x00, sizeof(unsigned int) * (m + 1));for (int i = 0; i < n; swap(lcs1, lcs2), i++)for (int j = 0; j < m; j++)lcs2[j + 1] = (A[i] == B[j]) ? 1 + lcs1[j] : max(lcs2[j], lcs1[j + 1]);unsigned int solu = lcs1[m];delete[] lcs1; delete[] lcs2;return solu;}
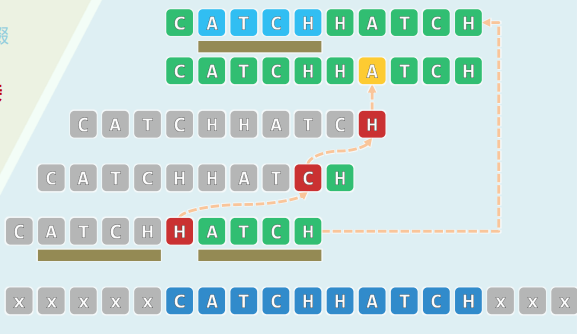
2. EP:就地循环移位
问题描述:仅用O(1)辅助空间,将数组A[0, n)中的元素向左循环移动k个单位
蛮力算法:
while (k--) shift(A, n, 0, 1);反复以1为间距循环左移,迭代版:按照同余类依次左移,时间复杂度
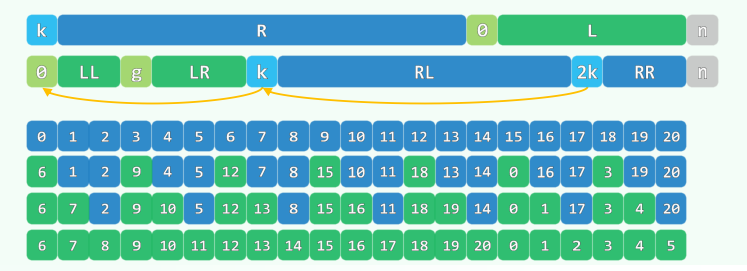
xxxxxxxxxxint shift( int * A, int n, int s, int k ) { //O(n/GCD(n, k))int b = A[s];int i = s, j = (s + k) % n;int mov = 0; //mov记录移动次数while ( s != j ) { //从A[s]出发,以k为间隔,依次左移k位A[i] = A[j];i = j;j = (j + k) % n;mov++;}A[i] = b;return mov + 1; //最后,起始元素转入对应位置} //[0, n)由关于k的g = GCD(n, k)个同余类组成,shift(s, k)能够且只能够使其中之一就位void shift1(int* A, int n, int k) { //经多轮迭代,实现数组循环左移k位,累计O(n + g)for (int s = 0, mov = 0; mov < n; s++) //O(g) = O(GCD(n, k))mov += shift(A, n, s, k);}倒置版:
reverse(A, k),reverse(A + k, n - k),reverse(A, n), 时间复杂度xxxxxxxxxxvoid shift2(int* A, int n, int k) {reverse(A, k); // O(3k/2)reverse(A + k, n - k); // O(3(n - k) / 2)reverse(A, n); // O(3n/2)}
2 向量
循秩访问 (Call-By-Rank)
抽象数据类型 (Abstract Data Type):数据模型 + 定义在该模型上的一组操作 数据结构 (Data Structure):基于某种特定语言,实现ADT的一整套算法 Application = Interface × Implementation 具体实现 (Implementation) + 实际应用 (Interface/Application)
2.1 基本语法
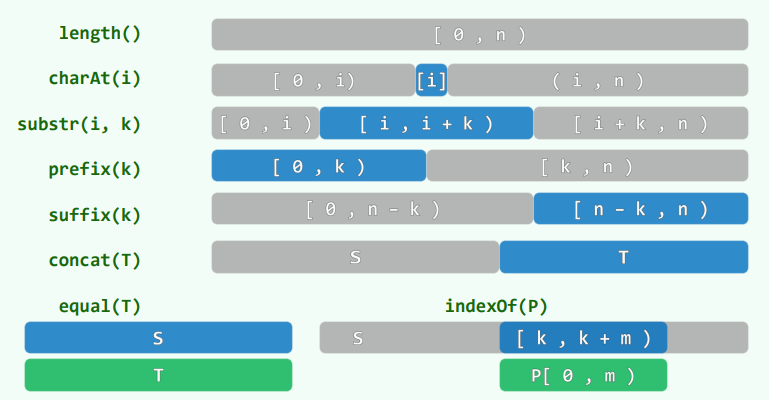
数组:元素由编号唯一指代并可以直接访问,称作线性数组 (Linear Array),访问方式称为寻秩访问 (call-by-rank),其中元素下标称为元素的秩(using Rank = int;)
向量:数组的抽象与泛化,由一组元素按线性次序封装而成;元素类型可以灵活选取
1. Vector ADT
vec.begin():0秩迭代器
vec.end():末秩迭代器
size():返回元素总数get(r):返回秩为r的元素put(r, e):用e替换秩为r元素的数值insert(r, e):e作为秩为r的元素插入,原先后继依次后移remove(r):删除秩为r的元素,返回该元素原值disordered():判断所有元素是否已经按非降序排列sort():调整各元素的位置,使之按非降序排列find(a):返回目标元素a的秩(如果不存在返回-1)search(e):返回不大于e且秩最大的元素(有序向量)deduplicate(), uniquify():剔除重复元素(无序/有序向量)traverse():遍历向量并统一处理所有元素,参数为函数对象或函数指针
2. Vector的构造与析构
(typename=T)
vec._capacity:容量
define DEFAULT_CAPACITY X:默认初始容量X
vec._size:元素总数
vec._elem:指向元素数组的指针
构造函数 默认构造函数:
Vector(int c = DEFAULT_CAPACITY) {_elem = new T[_capacity = c]; _size = 0;}数组区间复制:
Vector(T const * A, Rank lo, Rank hi) {copyFrom(A, lo, hi);}向量区间复制:Vector(Vector<T> const & V, Rank lo, Rank hi) {copyFrom(V._elem, lo, hi);}向量整体复制:Vector(Vector<T> const & V) {copyFrom(V._elem, 0, V._size);}copyFrom():_elem = new T[_capacity = max(DEFAULT_CAPACITY, 2*(hi - lo))];析构函数
~Vector{delete [] _elem;}
3. 动态空间管理
上溢 (overflow):_elem[]不足以存放所有元素
下溢 (underflow):_elem[]中的元素寥寥无几
装填因子 (load factor):
--扩容算法:expand()
xxxxxxxxxxtemplate <typename T>void Vector<T>::expand() { if (_size < _capacity) return; //尚未满员时不必扩容 _capacity = max(_capacity, DEFAULT_CAPACITY); //不低于最小容量 T* oldElem = _elem; _elem = new T[_capacity <<= 1]; //容量加倍 for (Rank i = 0; i < size; ++i) {_elem[i] = oldElem[i];} //复制 delete [] oldElem;} //得益于向量的封装,尽管扩容之后数据区的物理地址有所改变,却不致出现野指针--算法分析
平均分析 (average complexity):根据各种操作出现概率的分布,计算成本加权平均 各种可能的操作独立考察,割裂了操作之间的相关性和连贯性,往往不能准确评判dsa 分摊分析 (amortized complexity):连续实施足够多次操作,所需总体成本摊还至单次操作 忠实刻画可能出现的操作序列,更为精准地评判dsa
- 容量递增策略:时间成本
- 容量加倍策略:时间成本
4. 无序向量:基本操作的实现
元素访问:重载
[]运算符xxxxxxxxxxtemplate <typename T>T & Vector<T>::operator[](Rank r) {return _elem[r];}template <typename T>const T & Vector<T>::operator[](Rank r) const { // 仅限于右值return _elem[r];}插入元素:
insert(r, e)xxxxxxxxxxtemplate <typename T>Rank Vector<T>::insert(Rank r, T const & e) {expand(); //如有必要,扩容for (Rank i = _size; i > r; i--)_elem[i] = _elem[i - 1];_elem[r] = e; _size++; return r;}区间删除:
remove(lo, hi)xxxxxxxxxxtemplate <typename T>int Vector<T>::remove(Rank lo, Rank hi) { // [lo, hi)if (lo == hi) return 0; //出于效率考虑,单独处理退化情况while (hi < _size) _elem[lo++] = _elem [hi++];_size = lo;shrink(); //若有必要,缩容return hi - lo; //返回被删除元素的数目}单元素删除:
remove(Rank r)xxxxxxxxxxtemplate <typename T>T Vector<T>::remove(Rank r) {T e = _elem[r];remove(r, r + 1);return e; //返回被删除元素}判等器
xxxxxxxxxxtemplate <typename K, typename V>struct Entry {K key; V value; //键值Entry(K k = K(), V v = V()) : key(k), value(v) {}; //默认构造函数Entry(Entry<K,V> const& e) : key(e.key), value(e.value) {}; //拷贝bool operator==(Entry<K,V> const& e) {return key == e.key;}bool operator!=(Entry<K,V> const& e) {return key != e.key;}}有序向量:比较器(较判等器增加
<,>)顺序查找:
find(e, lo, hi)xxxxxxxxxxtemplate <typename T>Rank Vector<T>::find(T const & e, Rank lo, Rank hi) const {while ((lo < hi--) && (e != _elem[hi])); //逆向查找return hi; //返回值<lo即意味着失败;否则返回满足相等的最大秩}输入敏感 (input-sensitive):最好
去重:
deduplicate()xxxxxxxxxxtemplate <typename T>Rank Vector<T>::deduplicate() {Rank oldSize = _size;for (Rank i = 1; i < _size; ) {if (find(_elem[i], 0, i) < 0) i++;else remove(i);}return oldSize - _size; //返回删除的元素个数} //O(n^2)遍历:
traverse()xxxxxxxxxx//方法一:函数指针——只读或局部性修改template <typename T>void Vector<T>::traverse(void (*visit)(T&)) {for (Rank i = 0; i < _size; ++i)visit(_elem[i]);}//方法二:函数对象——全局性修改更便捷template <typename T> template <typename VST>void Vector<T>::traverse(VST & visit) {for (Rank i = 0; i < _size; ++i)visit(_elem[i]);}[EP/Increase]:
xxxxxxxxxxtemplate <typename T>struct Increase {virtual void operator()(T & e) {e++;}}template <typename T>void increase(Vector<T> & V) {V.traverse(Increase<T>();)}
5. 有序向量:基本操作的实现
用相邻逆序对的数目可以度量向量的紊乱程度
判断是否有序:
xxxxxxxxxxtemplate <typename T>void checkOrder(Vector<T> & V) { int unsorted = 0; V.traverse(CheckOrder<T>(unsorted, V[0])); //统计紧邻逆序对 if (unsorted > 0) printf("Unsorted with %d adjacent inversion(s)\n", unsorted); else printf("Sorted\n");}去重:
uniquify(),复杂度
xxxxxxxxxxtemplate <typename T>int Vector<T>::uniquify() {Rank i = 0, j = 0;while (++j < _size) {if (_elem[i] != _elem[j])_elem[++i] = _elem[j];}_size = ++i;shrink();return j - i;}
2.2 查找(有序向量)
更精细地评估查找算法的性能:查找长度(search length,关键码的比较次数)
1. 二分查找(版本A)
binary_search 平均查找长度 =
xxxxxxxxxxtemplate <typename T>static Rank binSearch(T* S, T const & e, Rank lo, Rank hi) {while (lo < hi) { //每步迭代可能要做两次比较判断,有三个分支Rank mi = (lo + hi) >> 1;if (e < S[mi]) hi = mi; //深入前半段[lo, mi)else if (S[mi] < e) lo = mi + 1; //深入后半段[mi + 1, hi)else return mi; //命中}return -1; //查找失败}Fibonacci_search 平均查找长度 =
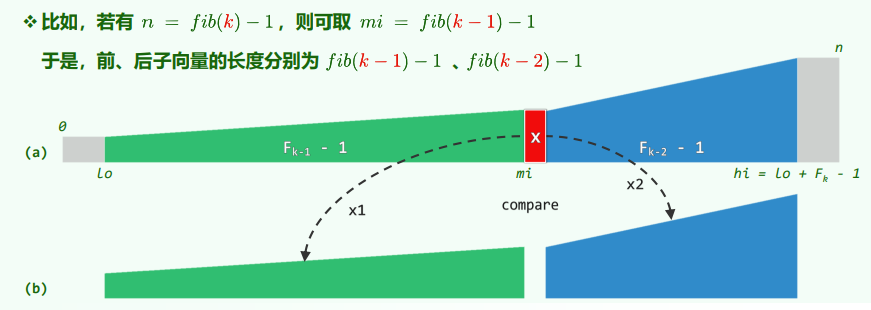
xxxxxxxxxxtemplate <typename T>static Rank fibSearch(T* S, T const & e, Rank lo, Rank hi) {for (Fib fib(hi - lo); lo < hi; ) { //Fib数列制表备查while (hi - lo < fib.get()) fib.prev(); //自后向前顺序查找轴点Rank mi = lo + fib.get() - 1; //确定形如Fib(k) - 1的轴点if (e < S[mi]) hi = mi; //深入前半段[lo, mi)else if (S[mi] < e) lo = mi + 1; //深入后半段(mi, hi)else return mi; //命中}return -1; //查找失败}通用策略:在任何区间
[0, n)内,总是选取递推式:
当
2. 二分查找(版本B)
相对于版本A,整体性能更趋均衡
xxxxxxxxxxtemplate <typename T>static Rank binSearch(T* S, T const & e, Rank lo, Rank hi) { while (1 < hi - lo) { Rank mi = (lo + hi) >> 1; e < S[mi] ? hi = mi; lo = mi; //区间分为[lo, mi)和[mi, hi) } return e == S[lo] ? lo : -1;}3. 二分查找(版本C)
较版本A和版本B优化了返回信息
返回信息:search(e)应该返回不大于e的最后一个元素,使得语句V.insert(1 + V.search(e), e)成立
xxxxxxxxxxtemplate <typename T>static Rank binSearch(T* S, T const & e, Rank lo, Rank hi) { while (lo < hi) { Rank mi = (lo + hi) >> 1; e < S[mi] ? hi = mi : lo = mi + 1; //[lo, mi)或[mi + 1, hi) } //出口时,必有S[lo = hi] return lo - 1;}证明:① 不变性:A[0, lo) ≤ e < A[hi, n),
在算法执行过程中的任意时刻,A[lo - 1]总是(截至目前已确认的)≤ e的最大者,A[hi]总是(截至目前已确认的)> e的最小者;算法结束时A[lo - 1] = A[hi - 1]是全局 ≤ e的最大者。
② 规模缩减
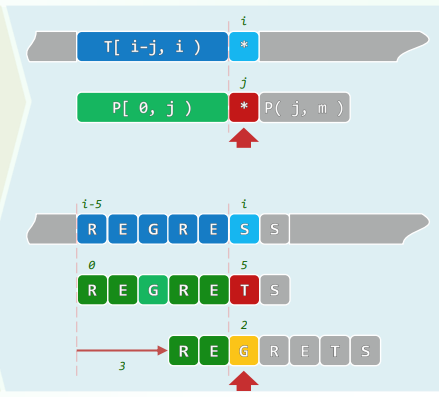
4. 插值查找
假设:已知有序向量中各元素随机分布的规律,如独立且均匀的随机分布
则[lo, hi]内各元素应大致呈线性趋势增长:
算法分析:
最坏情况:
插值查找:在字长意义上的折半查找 二分查找:在字长意义上的顺序查找
综合评价:
从
实际可行的方法:首先通过插值查找将查找范围缩小,然后再进行二分查找进一步缩小范围,最后在102数据范围采用顺序查找
2.3 排序
排序器:统一入口
xxxxxxxxxxtemplate <typename T>void Vector<T>::sort(Rank lo, Rank hi)- 起泡排序:bubbleSort:
- 归并排序:mergeSort:
- 选择排序:selectionSort:
- 插入排序:insertionSort:
- 堆排序:heapSort
- 快速排序:quickSort
- 希尔排序:shellSort
1. 起泡排序bubbleSort
复杂度:
基本版:
xxxxxxxxxxtemplate <typename T>Vector<T>::bubbleSort(Rank lo, Rank hi) { while (lo < --hi) { for (Rank i = lo; i < hi; ++i) if (_elem[i] > _elem[i + 1]) swap(_elem[i], _elem[i + 1]); }}提前终止版:
xxxxxxxxxxtemplate <typename T>void Vector<T>::bubbleSort(Rank lo, Rank hi) { for (bool sorted = false; sorted = !sorted; hi--) for (Rank i = lo + 1; i < hi; ++i) if (_elem[i - 1] > _elem[i]) { swap(_elem[i - 1], _elem[i]); sorted = false; //仍未完全有序 }}跳跃版:
xxxxxxxxxxtemplate <typename T>void Vector<T>::bubbleSort(Rank lo, Rank hi) { while (lo < (hi = bubble(lo, hi)); ) }template <typename T>Rank Vector<T>::bubble(Rank lo, Rank hi) { Rank last = lo; while (++lo < hi) if (_elem[lo - 1] > _elem[lo]) { last = lo; //逆序对只可能残留与[lo, last) swap(_elem[lo - 1], _elem[lo]); } return last; //返回最右侧的逆序对位置}
// 2022 latest versiontemplate <typename T>void Vector<T>::bubbleSort(Rank lo, Rank hi) { for (Rank last; lo < hi; hi = last) for (Rank i = (last = lo) + 1; i < hi; ++i) if (_elem[i - 1] > _elem[i]) swap(_elem[i - 1], _elem[last = i]);}// A[lo, last) <= A[last, hi)// A[last - 1] < A[last, hi)算法评价
时间效率:最好
重复元素的稳定性:满足(起泡排序中唯有相邻元素才可以交换)

2. 归并排序mergeSort
分而治之的思想,by J. von Neumann (1945)
复杂度:
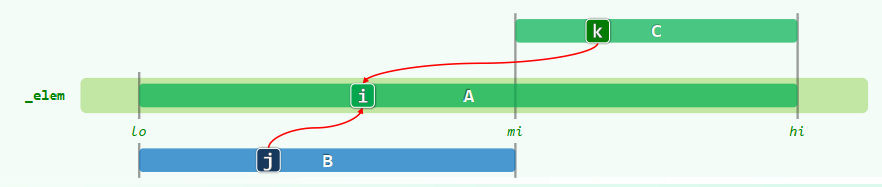
xxxxxxxxxxtemplate <typename T>void Vector<T>::mergeSort(Rank lo, Rank hi) { //[lo, hi) if (hi - lo < 2) return; int mi = (lo + hi) >> 1; mergeSort(lo, mi); mergeSort(mi, hi); merge(lo, mi, hi);}
template <typename T>void Vector<T>::merge(Rank lo, Rank mi, Rank hi) { Rank i = 0; T* A = _elem + lo; //A = _elem[lo, hi),就地 Rank j = 0, lb = mi - lo; T* B = new T[lb]; //B[0, lb) <-- _elem[lo, mi) for (Rank i = 0; i < lb; ++i) B[i] = A[i]; //复制自A的前缀 Rank k = 0, lc = hi - mi; T* C = _elem + mi; //C[0, lc) = _elem[mi, hi),就地 while ((j < lb) && (k < lc)) //反复的比较B,C的首元素 A[i++] = (B[j] <= C[k]) ? B[j++] : C[k++]; while (j < lb) //若C先耗尽 A[i++] = B[j++]; delete [] B;}算法评价
- 时间效率:
- 优点 只要实现恰当,可以保证稳定性 可拓展性极佳,适宜于外部排序(海量网页搜索结果的归并) 易于并行化
- 缺点
非就地,需要对等规模的辅助空间
即便输入接近有序,仍需要
2.4 位图:数据结构
有限整数集:实现三个主要功能bool test(int k);,void set(int k);,void clear(int k)
1. 位图dsa实现
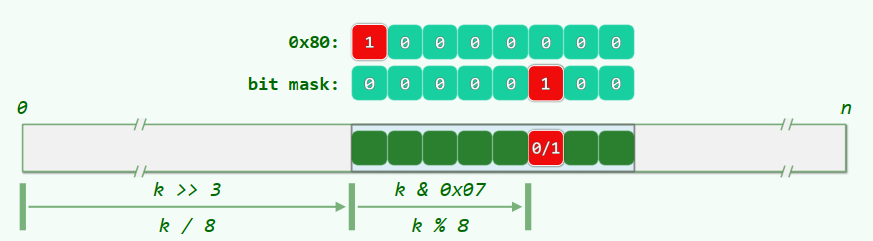
xxxxxxxxxxclass Bitmap {private: int N; unsigned char* M;public: Bitmap(int n = 8) { M = new unsigned char[N = (n + 7) / 8]; memset(M, 0, N); } ~Bitmap() {delete [] M; M = NULL;} void set(int k); //将k放入集合 void clear(int k); //集合中去除k void bool test(int k); //返回集合中是否存在k}
bool Bitmap::test(int k) { return M[k >> 3] & (0x80 >> (k & 0x07)); // k & 0x07 == k % 8 (bitmask)}void Bitmap::set(int k) { expand(k); M[k >> 3] |= (0x80 >> (k & 0x07));}void Bitmap::clear(int k) { expand(k); M[k >> 3] &= ~(0x80 >> (k & 0x07));}应用:小集合+大数据
int A[n]的元素均取自[0, m),已知数据规模不大但重复度极高,如何去重?
Idea1. 先排序,在扫描——
xxxxxxxxxxBitmap B(m); //S(m)for (int i = 0; i < n; ++i) B.set(A[i]); //O(n), 将第A[i]为置为1for (int i = 0; i < m; ++i) if (B.test(i)) ... //O(m), 判断A[i]是否存在2. 筛法
xxxxxxxxxxvoid Eratosthenes(int n, char* file) { Bitmap B(n); B.set(0); B.set(1); for (int i = 2; i < n; ++i) { if (!B.test(i)) //说明i是素数 for (int j = i * i; j < n; j += i) //可以改成i * i起点 B.set(j); } B.dump(file);}内循环每趟迭代
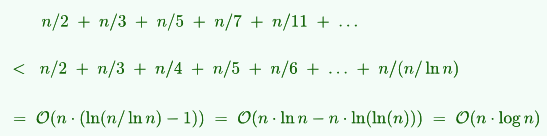
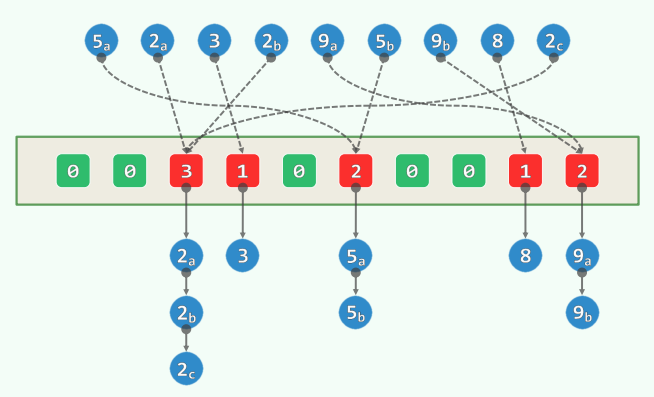
3. 快速初始化:校验环
结构:校验环(J. Hopcroft, 1974),将B[]拆分成一对等长的Rank型向量,有效位均满足:T[F[k]] = k, F[T[k]] = k,操作复杂度为
xxxxxxxxxxRank F[m]; //FromRank T[m]; Rank top = 0; //To及其栈顶指示
bool Bitmap::test(Rank k) { return (0 <= F[k]) && (F[k] < top) && (k == T[F[k]]);}void Bitmap::reset() { top = 0;}void Bitmap::set(Rank k) { if (!test(k)) {T[top] = k; F[k] = top++;}}void Bitmap::clear(Rank k) { if (test(k) && (--top)) { F[T[top]] = F[k]; T[F[k]] = T[top]; }}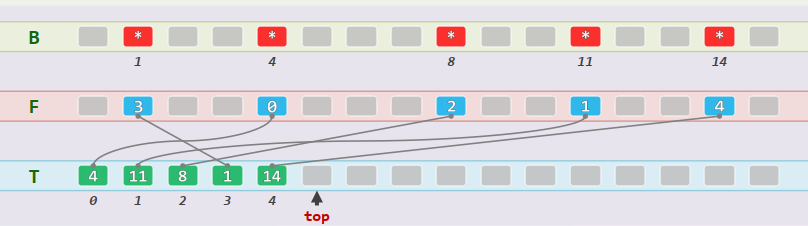
3 列表
循位置访问(Call-By-Position)
静态 vs 动态 数据结构 静态:仅读取,数据结构的内容及组成一般不变(
get,search) 数据空间整体创建或销毁 数据元素的物理存储次序与其逻辑次序严格一致,可支持高效的静态操作 动态:需写入,数据结构的局部或整体将改变(put,insert,remove) 为各数据元素动态地分配和回收的物理空间 相邻元素记录彼此的物理地址,在逻辑上形成一个整体,可支持高效的动态操作列表:采用动态储存策略的典型结构 节点 (node):列表中的元素,通过指针或引用彼此链接;在逻辑上构成一个线性序列 前驱 (predecessor) / 后继 (successor):相邻节点;没有前驱/后继的节点称作首 (first/front) / 末 (last/rear) 节点
3.1 ListNode ADT
xxxxxxxxxxtemplate <typename T> using ListNodePosi = ListNode<T>*;template <typename T> struct ListNode { T data; //数值 ListNodePosi<T> pred; //前驱 ListNodePosi<T> succ; //后继 ListNode() {} ListNode(T e, ListNodePosi<T> p = NULL, ListNodePosi<T> s = NULL) : data(e), pred(p), succ(s) {} ListNodePosi<T> insertAsPred(T const & e); //前插入 ListNodePosi<T> insertAsSucc(T const & e); //后插入};pred():当前节点前驱节点的位置succ():当前节点后继节点的位置data():当前节点所存数据对象insertAsPred(e):插入前驱节点,存入被引用对象e,返回新节点位置xxxxxxxxxxtemplate <typename T>ListNodePosi<T> ListNode<T>::insertAsPred(T const & e) {ListNodePosi<T> x = new ListNode(e, pred, this);pred->succ = x; pred = x;return x;}insertAsSucc(e):插入后继节点的,存入被引用对象e,返回新节点位置
3.2 List ADT
约定:头、首、末、尾节点的秩,分别理解为-1, 0, n-1, n
xxxxxxxxxxtemplate <typename T> class List {private: int _size; ListNodePosi<T> header, trailer; //哨兵 protected: void init() { header = new ListNode<T>; trailer = new ListNode<T>; header->succ = trailer; header->pred = NULL; trailer->pred = header; trailer->succ = NULL; _size = 0; } void copyNodes(ListNodePosi<T> p, int n) { init(); while (n--) { //将起自p的n项依次作为末节点 insertAsLast(p->data); p = p->succ; } } int clear() { int oldSize = _size; while (0 < _size) remove(header->succ); return oldSize; } public: List(List<T> const & L) { copyNodes(L.first(), L._size); } ~List() { clear(); delete header; delete trailer; } T operator[](Rank r) const { // assert: 0 <= r < size,T(r) = O(r) ListNodePosi<T> p = first(); //从首结点出发 while (0 < r--) p = p->succ; return p->data; } //秩 == 前驱的总数}
size():报告列表当前的规模(节点总数)first(), last():返回首、末节点的位置insertAsFirst(e), insertAsLast(e):将e当作首、末节点插入insert(p, e), insert(e, p):将e当作节点p的直接后继、前驱插入xxxxxxxxxxtemplate <typename T>ListNodePosi<T> List<T>::insert(T const & e, ListNodePosi<T> p) {_size++;return p->insertAsPred(e);}remove(p):删除位置p处的节点,返回其中数据项xxxxxxxxxxtemplate <typename T>T List<T>::remove(ListNodePosi<T> p) {T e = p->data; //备份p->pred->succ = p->succ;p->succ->pred = p->pred;delete p;_size--;return e; //返回备份的数值}disordered():判断所有节点是否已按非降序排列sort():调整各节点的位置,使之按非降序排列find(e):查找目标元素e,失败时返回NULLxxxxxxxxxxtemplate <typename T> // assert: 0 <= n <= rank(p) < _sizeListNodePosi<T> List<T>::find(T const & e, int n, ListNodePosi<T> p) const {while (0 < n--) // 自后向前if (e == (p = p->pred) -> data)return p; // 在p的n个前驱中,返回等于e的最靠后者return NULL;}template <typename T>ListNodePosi<T> List<T>::find(T const & e) const {return find(e, _size, trailer);}search(e)【有序列表】:查找e,返回不大于e且秩最大的节点xxxxxxxxxxtemplate <typename T>ListNodePosi<T> List<T>::search(T const & e, int n, ListNodePosi<T> p) const {do {p = p->pred;n--;} while ((-1 < n) && (e < p->data));return p; // 失败时,返回区间左边界的前驱(可能是header)} // 最好O(1),最坏O(n),平均O(n);无法通过有序性提高查找效率deduplicate(), uniquify():针对列表/有序列表,踢除重复节点xxxxxxxxxx//deduplicate(): O(n^2)template <typename T>int List<T>::deduplicate() {int oldSize = _size;ListNodePosi<T> p = first();for (Rank r = 0; p != trailer; p = p->succ)if (ListNodePosi<T> q = find(p->data, r, p))remove(q);else r++;return oldSize - _size;}//uniquify(): O(n)template <typename T>int List<T>::uniquify() {if (_size < 2) return 0;int oldSize = _size;ListNodePosi<T> p = first();ListNodePosi<T> q; // 各区段起点及其直接后继while (trailer != (q = p->succ)) // 反复考察紧邻的节点对(p, q)if (p->data != q->data) p = q;else remove(q);return oldSize - _size;}traverse():遍历列表xxxxxxxxxxtemplate <typename T>void List<T>::traverse(void (*visit)(T & )) {for (NodePosi<T> p = header->succ; p != trailer; p = p->succ)visit(p->data);}
3.3 排序
- 起泡排序:bubbleSort:
- 归并排序:mergeSort:
- 选择排序:selectionSort:
- 插入排序:insertionSort:
- 堆排序:heapSort
- 快速排序:quickSort
- 希尔排序:shellSort
1. 选择排序selectionSort
xxxxxxxxxxtemplate <typename T> void List<T>::selectionSort(ListNodePosi<T> p, int n) { ListNodePosi<T> head = p->pred, tail = p; for (int i = 0; i < n; ++i) tail = tail->succ; //待排序区间为(head, tail) while (1 < n) { // 反复从待排序区间内找出最大者,并移至有序区间前端 insert( remove( selectMax(head->succ, n) ), tail ); tail = tail->pred; n--; }}
template<typename T> // 起始于p的n各元素中选出最大者ListNodePosi<T> List<T>::selectMax(ListNodePosi<T> p, int n) { ListNodePosi<T> max = p; for (ListNodePosi<T> cur = p; 1 < n; n--) if (! lt( (cur = cur->succ)->data, max->data)) // data >= max max = cur; return max;}// 稳定性:有多个元素同时命中时,约定返回其中特定的某一个(比如最靠后者)// 采用比较器!lt()或ge(),从而等效于后者优先性能分析:
- 共迭代n次,在第k次迭代中
selectMax():swap(): - 尽管如此,元素的移动操作远远少于起泡排序(选择排序的
- 改进方向:利用高级的数据结构,
selectMax()可改进至
2. 循环节/Cycle
Definition:
任何一个序列
,都可以分解为若干个循环节 任何一个序列 ,都对应于一个有序序列 元素 在 中对应的秩,记作 元素 所属的循环节是: 每个循环节,长度均不超过 循环节之间,互不相交
Analysis:
- 采用交换法,每迭代(
swap())一步,M都会脱离原属的循环节,自成一个循环节 - “
3. 插入排序insertionSort
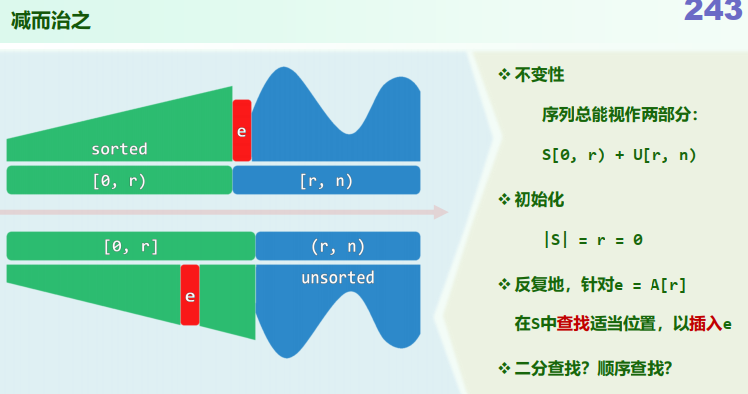
xxxxxxxxxxtemplate <typename T>void List<T>::insertionSort(ListNodePosi<T> p, int n) { for (int r = 0; r < n; ++r) { insert( search(p->data, r, p), p->data ); p = p->succ; remove(p->pred); } // n次迭代,每次O(r + 1)} // 仅使用O(1)的辅助空间,属于就地算法性能分析:
若各元素的取值系独立均匀分布,平均要做多少次元素比较? 考察
刚插入完成的那一时刻,此时的有序前缀 中,谁是 ? 观察:其中的 个元素都有可能,且概率均为 因此,在刚完成的这次迭代中,为引入 所花费时间的数学期望为: 于是,总体时间的数学期望为 Case Sensitive best case =
worst case =
4. 归并排序mergeSort
时间复杂度:
xxxxxxxxxxtemplate <typename T>void List<T>::mergeSort(ListNodePosi<T> & p, int n) { if (n < 2) return; ListNodePosi<T> q = p; int m = n >> 1; //以中点为界 for (int i = 0; i < m; ++i) q = q->succ; mergeSort(p, m); mergeSort(q, n - m); //子序列分别排序 p = merge(p, m, *this, q, n - m); //归并}
template <typename T>ListNodePosi<T> List<T>:: merge(ListNodePosi<T> p, int n, List<T> & L, ListNodePosi<T> q, int m) { ListNodePosi<T> pp = p->pred; //归并之后p或不再指向首节点,故需先记忆,以便返回前更新 while ( (0 < m) && (q != p) ) //小者优先归入 if ( (0 < n) && (p->data <= q->data) ) { p = p->succ; n--; } else { insert( L.remove( (q = q->succ)->pred ), p ); m--; } return pp->succ;} // 时间复杂度:O(n + m),线性正比于节点总数5. 逆序对/Inversion
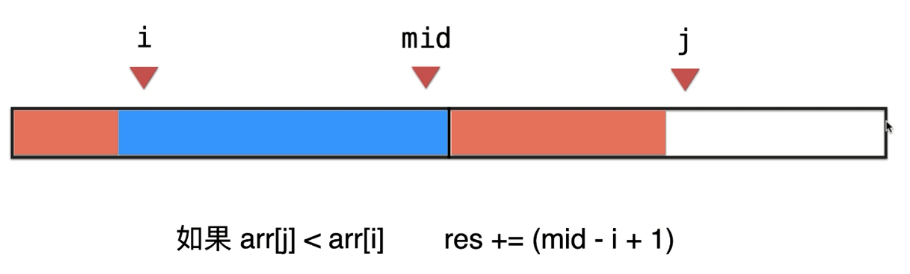
Definition:
逆序对总数:
对于BubbleSort来说,交换操作的次数恰好等于输入序列所含逆序对的总数
对于InsertionSort来说,针对
任意给定一个序列,统计其中逆序对的总数: 采用归并排序,仅需
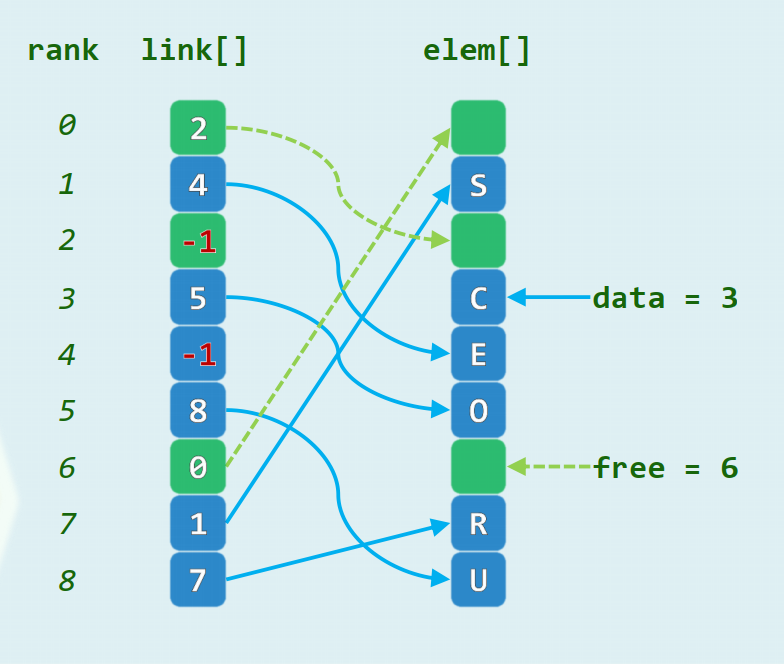
3.4 游标实现
利用线性数组,以游标方式模拟列表
elem[]:对外可见的数据项link[]:数据项之间的引用
维护逻辑上互补的列表data和free
insert()操作的时间复杂度为remove()操作的时间复杂度为
3.5 Java和Python的列表实现
4 栈与队列
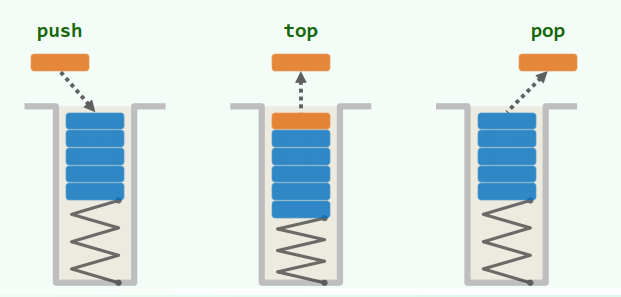
栈(stack):是受限的序列 只能在栈顶(top)插入和删除 栈底(bottom)为盲端 后进先出(LIFO)
4.1 栈及其基本运用
基本接口
size() / empty():判断大小 / 判断是否为空
push():入栈
pop():出栈
top():查顶
扩展接口:getMax()......
- 属于序列的特例,可以直接基于向量或列表派生
xxxxxxxxxxtemplate <typename T>class Stack : public Vector<T> {public: //原有接口一概沿用 void push(T const & e) {insert(e);} //入栈 T pop() {return remove(size() - 1);} //出栈 T & top() {return (*this)[size() - 1];} //取顶}; //以向量首/末端为栈底/顶- 也可以通过继承
List来实现 - 如此实现的栈的各接口,均只需
递归
空间复杂度:递归算法所需的空间,主要取决于递归的深度,而非递归实例总数
1. 消除递归:尾递归
定义:在递归实例中,作为最后一步的递归调用
是最简单的递归模式 一旦抵达递归基,便会引发一连串的return(且返回地址相同),调用栈相应地连续pop 编译器一般可以自动识别并代为改写为迭代形式 改用迭代形式:时间复杂度有常系数改进,空间复杂度或有渐近改进
以阶乘为例:

2. 进制转换
实现难点:位数
xxxxxxxxxxvoid convert(Stack<char> & S, __int64 n, int base) { char digit[] = "0123456789ABCDEF"; // 数位符号,如有必要可相应扩充 while (n > 0) { S.push( digit[n % base] ); n /= base; // 余数入栈,n更新为除商 } // 新进制下由高到低的各数位,自顶而下保存于栈S中}
int main() { Stack<char> S; convert(S, n, base); // 用栈记录转换得到的各数位 while (!S.empty()) printf("%c", S.pop()); // 逆序输出}3. 括号匹配
算法思路:顺序扫描表达式,用栈记录已扫描的部分——反复迭代(遇到(则进栈,遇到)则出栈)
xxxxxxxxxxbool paren(const char exp[], int lo, int hi) { // exp[lo, hi) Stack<char> S; for (int i = lo; i < hi; ++i) { if ('(' == exp[i]) S.push(exp[i]); else if (!S.empty()) S.pop(); // 遇右括号:若栈非空,则弹出对应的左括号 else return false; //否则(遇到右括号时栈已空,必不匹配 } return S.empty();}实际上,若仅考虑一种括号,只需一个计数器足矣:S.size()
一旦转负,则为适配(右括号多余); 最后不为零,则不匹配(左括号多余); 最后归零,即为匹配
扩展:多类括号
只需约定“括号”的通用格式,而不必实现固定括号的类型与数量
[EX/html]:<body> | </body>, <h1> | </h1>, <font> | </font>, <p> | </p>...
4. 栈混洗 Stack Permutation
栈混洗:将栈A中的元素全部转入栈B中(S.push(A.pop()); B.push(S.pop()))
Notation:
计数:SP(n)
同一输入序列,可有多种栈混洗。一般地,对于长度为
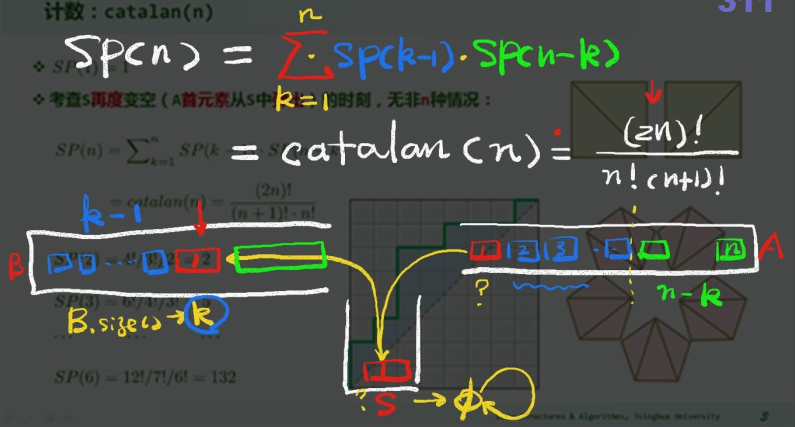
甄别禁形
禁形:对任何
- 充要性(Knuth, 1968):A permutation is a stack permutation iff it does NOT involve the permutation 312
- 如此,可得一个
- 如此,可得一个
S.pop()之前,检测S是否已空;或需弹出的元素在S中,却非顶元素:
括号匹配 观察:每一栈混洗,都对应于栈S的n次push与n次pop操作构成的某一序列;反之亦然 n个元素的栈混洗,等价于n对括号的匹配;二者的组合数,也自然相等
4.2 表达式求值
1. 中缀表达式求值
思路:自左向右扫描表达式,用栈记录已扫描的部分(含已执行运算的结果)
栈的顶部存在可优先计算的子表达式 ? 该子表达式推展;计算其数值;计算结果进栈 : 当前字符进栈,转入下一字符
xxxxxxxxxxdouble evaluate(char* S, char* RPN) { // S保证语法正确 Stack<double> opnd; // 运算数栈 Operand Stack Stack<char> optr; // 运算符栈 Operator optr.push('\0'); while (!optr.empty()) { if (isdigit(*S)) // 若为操作数 readNumber(S, opnd); // 读入 else // 若为运算符,则视其与栈顶运算符之间优先级的高低 switch(priority(optr.top(), *S)) { //见“优先级表” case '<': // 栈顶运算符优先级更低 optr.push(*S); S++; break; // 计算推迟,当前运算符进栈 case '=': // 优先级相等(当前运算符为右括号,或尾部哨兵'\0') optr.pop(); // 脱括号并接收下一个字符 S++; break; case '>': char op = optr.pop(); if ('!' == op) opnd.push(calcu(op, opnd.pop())); // 一元运算符 else { double opnd2 = opnd.pop(), opnd1 = opnd.pop(); //二元运算符 opnd.push( calcu(opnd1, op, opnd2) ); // 实施计算。结果入栈 } break; } } return opnd.pop(); // 弹出并返回最后的计算结果}
2. 逆波兰表达式 Reverse Polish Notation / RPN
逆波兰表达式:J. Lukasiewicz (1878 ~ 1956) 由运算符 (operator) 和操作数 (operand) 组成的表达式中,不需要括号 (parenthesis-free),即可表示带优先级的运算关系 作为补偿,须额外引入一个起分割作用的元字符(比如空格)
亦称作后缀式 (postfix)
应用:PostScript (1985),支持设备独立的图形描述 (1 × 解释器 + 5 × 栈)× RPN语法
xxxxxxxxxx// pseudo code引入栈S //存放操作数逐个处理下一个元素 if (x是操作数) 将x压入S else //运算符无需缓冲 从S中弹出x所需数目的操作数 执行相应的计算,结果压入S //无需估计优先级返回栈顶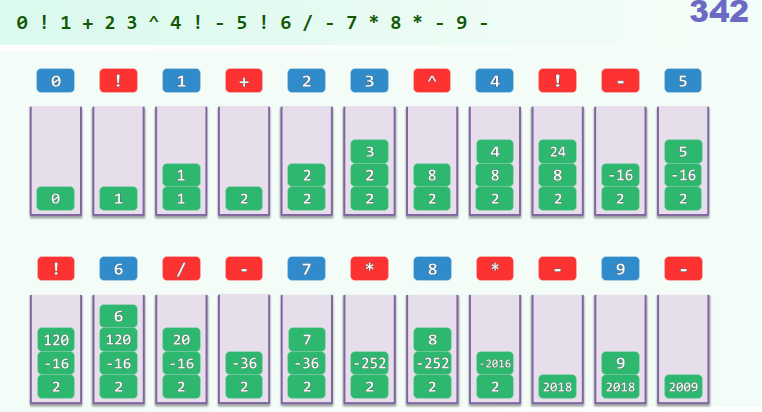
xxxxxxxxxxdouble evaluate(char* S, char* RPN) { // RPN转换 while (!optr.empty()) { if (isdigit(*S)) { readNumber(S, opnd); append(RPN, opnd.top()); //将其接入RPN } else //若当前字符为运算符 switch(priority(optr.top(), *S)) { /*...*/ case '>': { char op = optr.pop(); append(RPN, op); } /*...*/ } }}
4.3 队列
队列(queue):受限的序列
只能在队尾插入 / 查询:
enqueue(),rear()只能在队头删除 / 查询:dequeue(),front()先进先出 (FIFO): First in First out 后进后出 (LILO): Last in Last out
扩展接口:
getMax()...
基本接口
bool empty():判空
void enqueue(T const& e):队尾插入
T dequeue():队头删除
T front():查询队头元素
int size():查询队列长度
属于序列的特例,可以直接基于向量或列表派生
xxxxxxxxxxtemplate <typename T>class Queue : public List<T> {public:void enqueue(T const & e) { insertAsLast(e); } // 入队T dequeue() { return remove(first()); } // 出队T & front() { return first()->data; } //队首查询}如此实现的队列接口,均只需
1. 资源循环分配
xxxxxxxxxx// RoundRobinQueue Q(clients); // 共享资源的所有客户组成队列while (!ServiceClosed()) { // 在服务关闭之前,反复地 e = Q.dequeue(); // 令队首的客户出队,并 serve(e); //接受服务, Q.enqueue(e); //然后重新入队}2. 银行服务模型
提供
个服务窗口: 任一时刻,每个窗口至多接待一位顾客,其他顾客排队等候 顾客到达后,自动地选择和加入最短队列(的末尾)
xxxxxxxxxx// 参数:nWin == 窗口/队列的数目,servTime == 营业时长struct Customer { // 顾客类 int window; //所处窗口(队列) unsigned int time; //服务市场};
void simulate(int nWin, int servTime) { Queue<Customer>* windows = new Queue<Customer>[nWin]; for (int now = 0; now < servTime; now++) { Customer c; c.time = 1 + rand() % 50; c.window = bestWindow(windows, nWin); // 找出最佳/最短服务窗口 windows[c.window].enqueue(c); //新顾客加入对应的队列 for (int i = 0; i < nWin; ++i) { if (!windows[i].empty()) { if (--windows[i].front().time <= 0) // 队首顾客接受服务 windows[i].dequeue(); //服务完毕则出列,有后继顾客接替 } } } delete [] windows; // 释放所有队列}3. 双栈当队
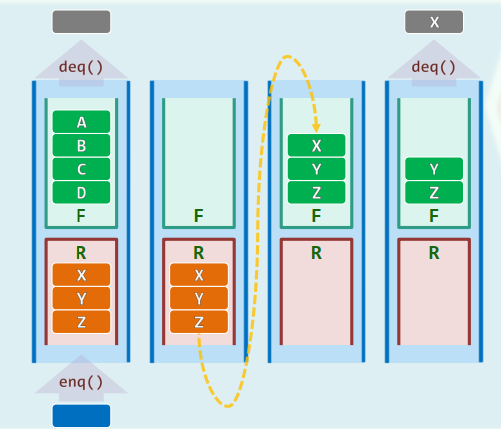
Queue = Stack × 2
xxxxxxxxxxdef Q.enqueue(e): R.push(e);def Q.dequeue(): // 0 < Q.size() if (F.empty()) while (!R.empty()) F.push(R.pop()); return F.pop();Best / Worse case:
Amortized Cost (of any operation sequence involving n items) =
Aggregate Cost = ( denotes enqueue()times,denotes dequeue()times) the amortized cost for each OPERATION isAmortization by Potential: Consider the operation Define Then Hence
4. Steap + Queap
Steap = Stack + Heap
P中每个元素,都是S中对应后缀里的最大者
xxxxxxxxxxSteap::getMax() { return P.top(); }Steap::pop() { P.pop(); return S.pop(); } // O(1)Steap::push(e) { P.push( max(e, P.top()) ); S.push(e); } // O(1)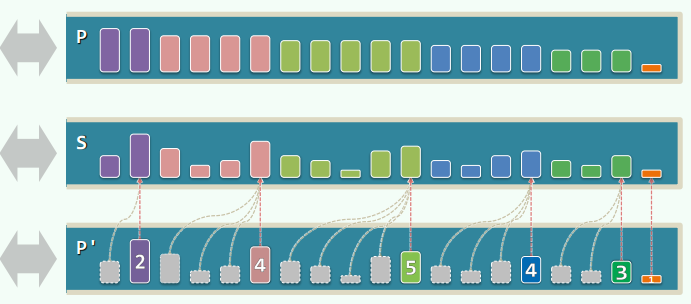
改进:构造p'队列,记录相同最大值的数量大小,从后往前扫描时只需累加并合并即可,分摊复杂度可以下降。
Queap = Queue + Heap
P中每个元素,都是Q中对应后缀的最大者
xxxxxxxxxxQueap::dequeue() { P.dequeue(); return Q.dequeue(); } // O(1)Queap::enqueue(e) { Q.enqueue(e); P.enqueue(e); for (x = P.rear(); x && (x->key <= e); x = x->pred ) // 最坏情况O(n) x->key = e;}*Double Ending Queue (Deq)*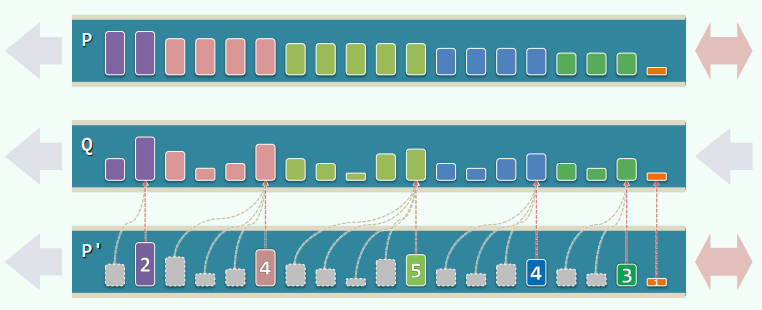
5. 直方图内最大矩形
Maximum: 全局最大值 Maximal: 局部极大值
Maximal rectangle supported by H[r]:
依次扫描所有
复杂度:

Using Stack
xxxxxxxxxxint* s = new int[n];Stack<Rank> S;// Determine s(r)for (int r = 0; r < n; r++) {while (!S.empty() && H[S.top()] >= H[r]) S.pop(); // until H[top] < H[r]s[r] = S.empty() ? 0 : 1 + S.top();S.push(r); // S is always ascending}while (!S.empty()) S.pop();// Determine t(r) by another scan in the REVERSED direction// By amortization, time complexity is O(n)维护一个单调递增的栈(栈顶元素即为待进栈
Problem:
One-Pass Scan:
xxxxxxxxxxStack<int> SR;__int64 maxRect = 0; // SR.2ndTop() == s(r) - 1 & Sr.top() == rfor (int t = 0; t <= n; t++) {while (!SR.empty() && (t == n || H[SR.top()] > H[t])) {int r = SR.pop();int s = SR.empty() ? 0 : SR.top() + 1;maxReact = max(maxRect, H[r] * (t - s));}if (t < n) SR.push(t);}return maxRect;每次进栈可以确定

5 二叉树
一种半线性的数据结构(在确定某种次序之后,具有线性特征)
树
树是极小连通图、极大无环图
指定任一节点
相对于
若指定
路径长度即所含边数:
如果覆盖所有节点各一次,则称作周游(tour)
连通图:节点之间均有路径(connected)。若连通图不含环路,则称为无环图(acyclic)
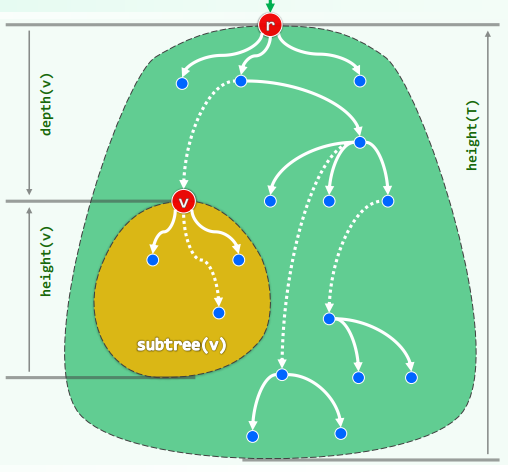
树的任一节点
根节点是所有节点的公共祖先,深度为
特别地,空树的高度取作
于是以
半线性:在任一深度,
二叉树
二叉树:有根有序树
节点度数不超过2
孩子(子树)可以左、右区分(隐含有序)
lc()~lSubtree()rc()~rSubtree()基数:设度数为
特别地,当
满树 深度为
特殊情况:
真二叉树 通过引入
如此转换之后,全树自身的复杂度并未实质增加
二叉树/多叉树的描述
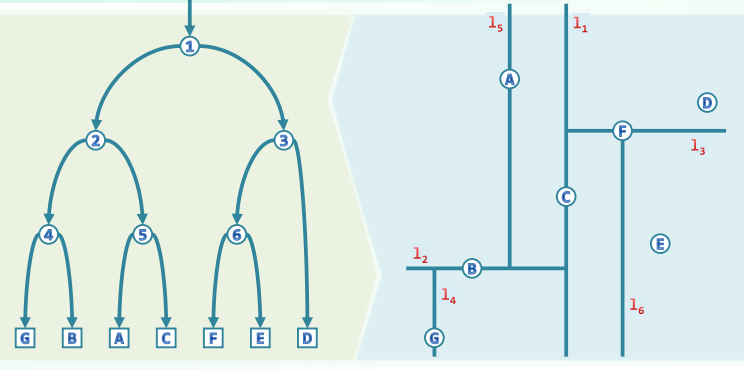
二叉树的描述
root():根节点parent():父节点firstChild():长子nextSibling():兄弟insert(i, e):将remove(i):删除第traverse():遍历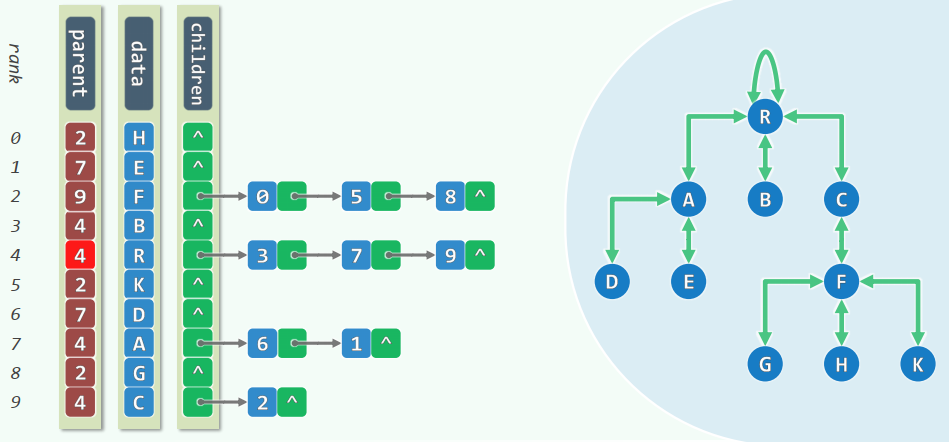
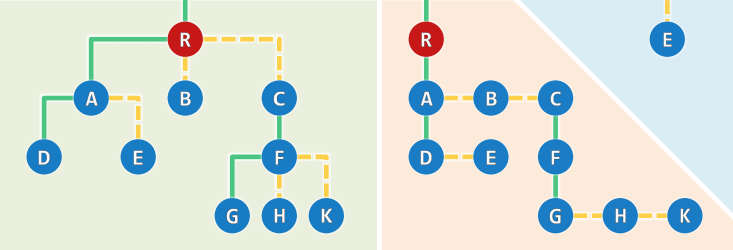
多叉树的描述:长子-兄弟表示法
有根且有序的多叉树,均可转化并表示为二叉树
- 长子 ~ 左孩子:
firstChild()~lc() - 兄弟 ~ 右孩子:
nextSibling()~rc()
- 长子 ~ 左孩子:
5.1 二叉树的实现
基本接口
BinNode模板类
xxxxxxxxxxtemplate <typename T> using BinNodePosi = BinNode<T>*;template <typename T> struct BinNode {BinNodePosi<T> parent, ls, rc; //父亲、孩子T data; int height;int size() { // 后代总数int s = 1; //计入本身if (lc) s += lc->size();if (rc) s += rc->size();return s;}BinNodePosi<T> insertAsLc(T const & e) { //作为左孩子插入新节点return lc = new BinNode(e, this);}BinNodePosi<T> insertAsRC(T const & e) { //作为有孩子插入新节点return rc = new BinNode(e, this);}BinNodePosi<T> succ(); //(中序遍历意义下)当前节点的直接后继template <typename VST> void travLevl(VST &); //层次遍历template <typename VST> void travPre(VST &); //先序遍历template <typename VST> void travIn(VST &); //中序遍历template <typename VST> void travPost(VST &); //后序遍历}BinTree模板类
xxxxxxxxxx//节点高度——空树~-1template <typename T> class BinTree {protected:int _size; //规模BinNodePosi<T> _root; //根节点virtual int updateHeight(BinNodePosi<T> x) { //更新节点x的高度return x->height = 1 + max( stature(x->lc), stature(x->rc) );}void updateHeightAbove(BinNodePosi<T> x); { //更新x及其祖先的高度while (x) { // O(n = depth(x))updateHeight(x);x = x->parent; //可优化}}public:int size() const { return _size; } //规模bool empty() const { return !_root; } //判空BinNodePosi<T> root() const { return _root; } //树根//孩子接入BinNodePosi<T> insert(BinNodePosi<T> x, T const & e); //右孩子BinNodePosi<T> insert(T const & e, BinNodePosi<T> x) { //左孩子_size++;x->insertAsLC(e);updateHeightAbove(x);return x->lc;}//子树接入BinNodePosi<T> attach(BinTree<T>* &S, BinNodePosi<T> x); //接入左子树BinNodePosi<T> attach(BinNodePosi<T> x, BinTree<T>* &S) { //接入右子树if (x->rc = S->_root)x->rc->parent = x;_size += S->_size;updateHeightAbove(x);S->root = NULL;S->_size = 0;release(S); S = NULL;return x;}//子树删除int remove(BinNodePosi<T> x) {FromParentTo(*x) = NULL;updateHeightAbove(x->parent); //更新祖先高度(其余节点亦不变)int n = removeAt(x);_size -= n;return n;}static int removeAt(BinNodePosi<T> x) {if (!x) return 0;int n = 1 + removeAt(x->lc) + removeAt(x->rc);release(x->data); release(x);return n;}//子树分离BinTree<T> secede(BinNodePosi<T> x) {FromParentTo( * x ) = NULL;updateHeightAbove( x->parent );// 以上与BinTree<T>::remove()一致;以下还需对分离出来的子树重新封装BinTree<T> * S = new BinTree<T>; //创建空树S->_root = x; x->parent = NULL; //新树以x为根S->_size = x->size(); _size -= S->_size; //更新规模return S; //返回封装后的子树}}
以下遍历其实都是深度优先搜索
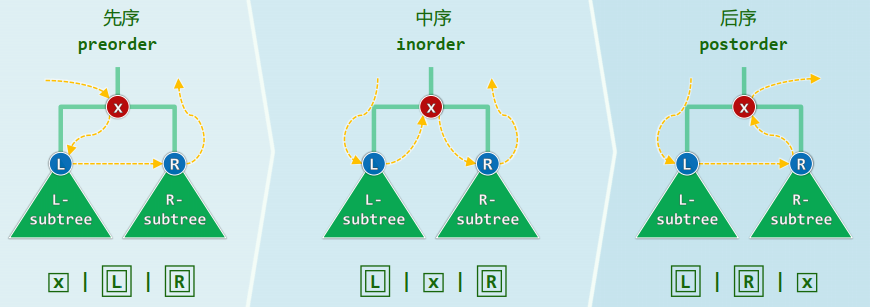
1. 先序遍历
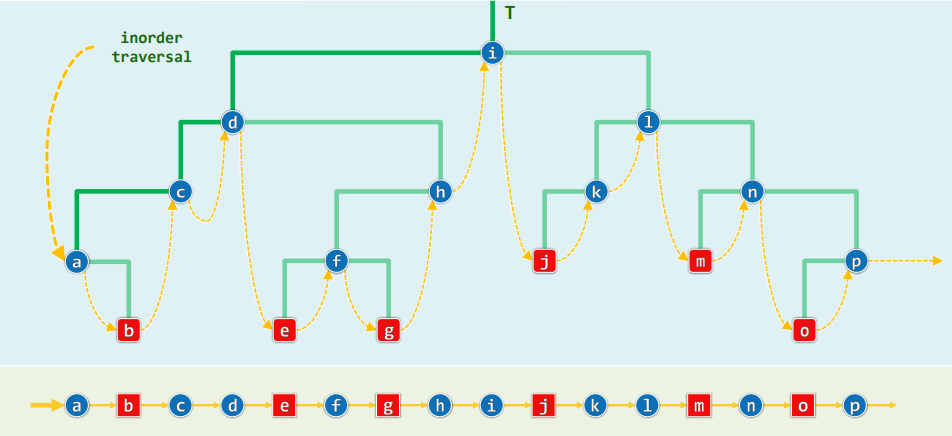
xxxxxxxxxxtemplate <typename T, typename VST>void traverse( BinNodePosi<T> x, VST & visit ) { if (!x) return; visit(x->data); traverse(x->lc, visit); traverse(x->rc, visit);} //O(n)Problem: 使用默认的Call Stack,允许的递归深度有限 改进:藤缠树
沿着左侧藤,自上而下访问藤上节点,自下而上遍历各右子树 各右子树的遍历彼此独立,自成一个子任务
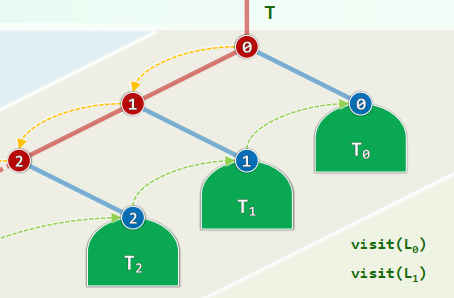
xxxxxxxxxxtemplate <typename T, typename VST>void travPre(BinNodePosi<T> x, VST & visit) { Stack<BinNodePosi<T>> S; //辅助栈 while (true) { while (x) { visit(x->data); S.push(x->rc); x = x->lc; } if (S.empty()) break; //栈空即退出 x = S.pop(); } //#pop = #push = #visit = O(n) = 分摊O(1)}2. 中序遍历
xxxxxxxxxxtemplate <typename T, typename VST>void traverse(BinNodePosi<T> x, VST & visit) { if (!x) return; traverse(x->lc, visit); visit(x->data); traverse(x->rc, visit);} //T(n) = T(a) + O(1) + T(n - a - 1) = O(n)藤缠树
沿着左侧藤,遍历可自底而上分解为
步迭代:访问藤上节点,再遍历其右子树 各右子树的遍历彼此独立,自成一个子任务
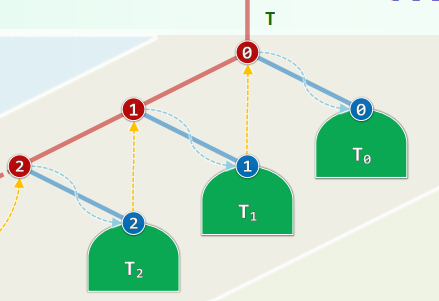
xxxxxxxxxxtemplate <typename T, typename V>void travIn(BinNodePosi<T> x, V & visit) { Stack<BinNodePosi<T>> S; //辅助栈 while (true) { while (x) { S.push(x); x = x->lc; } if (S.empty()) break; x = S.pop(); visit(x->data); x = x->rc; }}效率:分摊分析
每次迭代,都恰有一个节点出栈并被访问 每个节点入栈一次且仅一次 每次迭代所需要的时间...——分摊
分摊复杂度:
后继与前驱
xxxxxxxxxx// for (BinNodePosi<T> t = first(); t; t = t->succ()) ...// 在中序遍历移一下的直接后继template <typename T>BinNodePosi<T> BinNode<T>::succ() { BinNodePosi<T> s = this; if (rc) { s = rc; //若有右孩子,则直接后继必是右子树中的最小节点 while (HasLChild(*s)) s = s->lc; } else { //否则,后继应是“以当前节点为直接前驱者” while (IsRChild(*s)) s = s->parent; //不断朝左上移动 s = s->parent; //最后再朝右上移动一步 } return s;} //两种情况下,时间复杂度分别为当前节点的高度与深度,不过O(h)
3. 后序遍历
xxxxxxxxxxtemplate <typename T, typename VST>void traverse(BinNodePosi<T> x, VST & visit) { if (!x) return; traverse(x->lc, visit); traverse(x->rc, visit); visit(x->data);} //T(n) = T(a) + T(n - a - 1) + O(1) = O(n)藤缠树
从根出发下行:尽可能沿左分支,实不得已才沿右分支 最后一个节点必定是叶子,而且是按中序遍历次序最靠左者,也是递归版中
visit()首次执行处
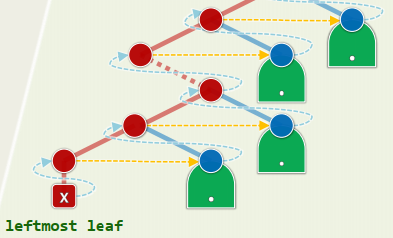
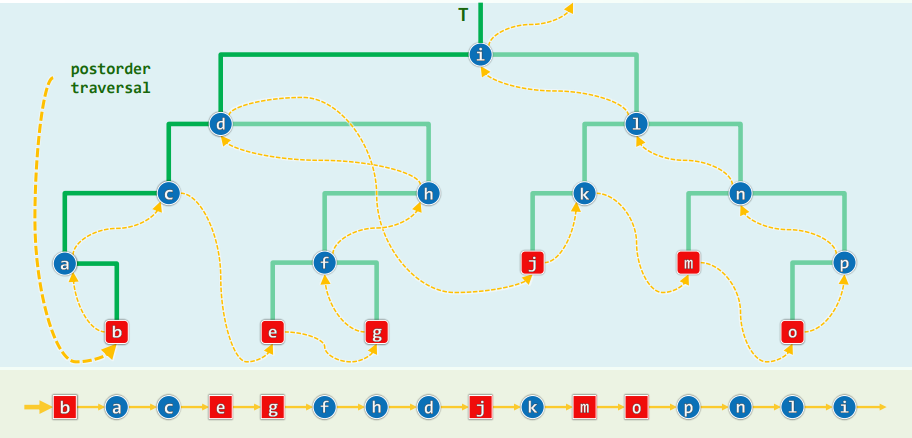
xxxxxxxxxxtemplate <typename T, typename V>void travPost(BinNodePosi<T> x, V & visit) { Stack<BinNodePosi<T>> S; //辅助栈 if (x) S.push(x); //根节点首先入栈 while (!S.empty()) { if (S.top() != x->parent) { //即栈顶为右兄,在右兄子树中找到最靠左的叶子 while (x = S.top()) if (HasLChild(*x)) { //尽可能向左,在此之前 if (HasRChild(*x)) //若有右孩子,则 S.push(x->rc); //优先入栈 S.push(x->lc); //然后转向左孩子 } else S.push(x->rc); //实不得已,转向右孩子 S.pop(); //返回之前,弹出栈顶的空节点 } x = S.pop(); //弹出栈顶(即前一节点的后继)以更新x visit(x->data); }}正确性:数学归纳法
每个结点出栈后:以之为根的子树已经完全遍历,而且其右兄弟r若存在,必恰在栈顶 此时正开始遍历子树r
效率:分摊分析
每次迭代,都有一个节点出栈并被访问 每个节点入栈一次且仅一次 每次迭代所需时间...
分摊复杂度:
表达式树(RPN)
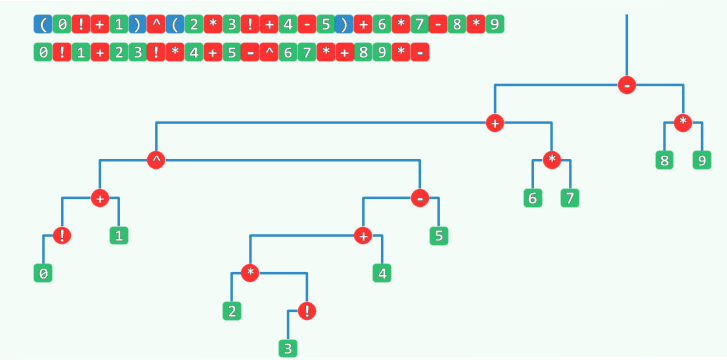
RPN实际上是Expression Tree的后序遍历
4. 层次遍历(广度优先)
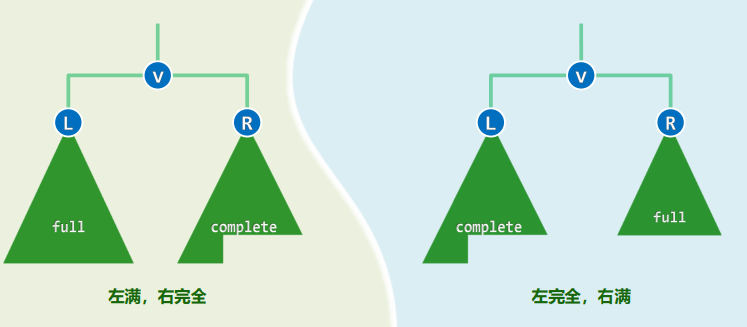
概念区分:满二叉树、完全二叉树、真二叉树
完全二叉树 叶节点仅限于最低两层 底层叶子,均居于次底层叶子左侧(相当于LCA) 除末节点的父亲,内部节点均有双子
叶节点:不致少于内部节点,但至多多出一个
xxxxxxxxxxtemplate <typename T> template <typename VST>void BinNode<T>::travLevel( VST & visit ) { //二叉树层次遍历 Queue< BinNodePosi<T> > Q; //引入辅助队列 Q.enqueue( this ); //根节点入队 while ( ! Q.empty() ) { //在队列再次变空之前,反复迭代 BinNodePosi<T> x = Q.dequeue(); //取出队首节点,并随即 visit( x->data ); //访问之 if ( HasLChild( * x ) ) Q.enqueue( x->lc ); //左孩子入队 if ( HasRChild( * x ) ) Q.enqueue( x->rc ); //右孩子入队 }}考察遍历过程中的n步迭代... 前
步迭代中,均有右孩子入队 前 步迭代中,都有左孩子入队 累计至少 次入队 辅助队列的规模: 先增后减,单峰且对称 最大规模 =
,最大规模可能出现2次
树的层次遍历 => 向量的顺序遍历
完全二叉树与满树
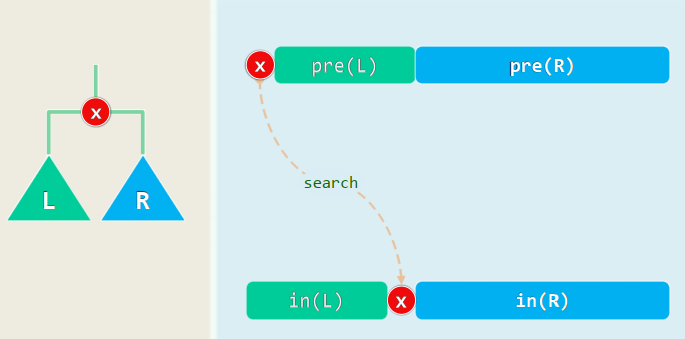
5.2 二叉树的重构
1. 先序 | 后序 => 中旭
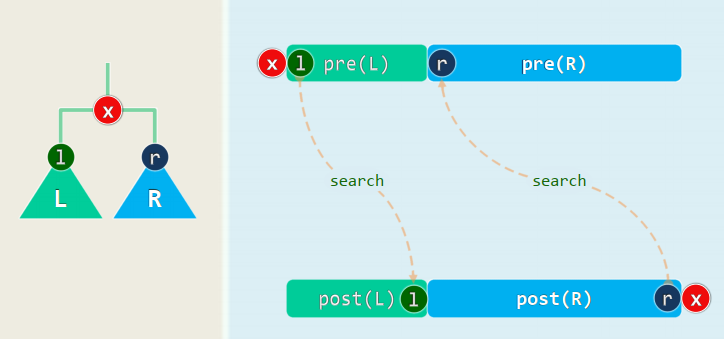
2. 先序 <=> 后序
3. 增强序列
假想地认为,每个NULL也是“真实”节点,并在遍历时一并输出 每次递归返回,同时输出一个事先约定的元字符“^”
若将遍历序列表示为一个Iterator,则可将其定义为Vector<BinNode<T>*>,于是在增强的遍历序列中,这类“节点”可统一记作NULL
可归纳证明:在增强的先序、中序、后序遍历序列中 1)任一子树依然对应于一个子序列,而且 2)其中的NULL节点恰比非NULL节点多一个
如此,通过对增强序列分而治之,即可重构原树
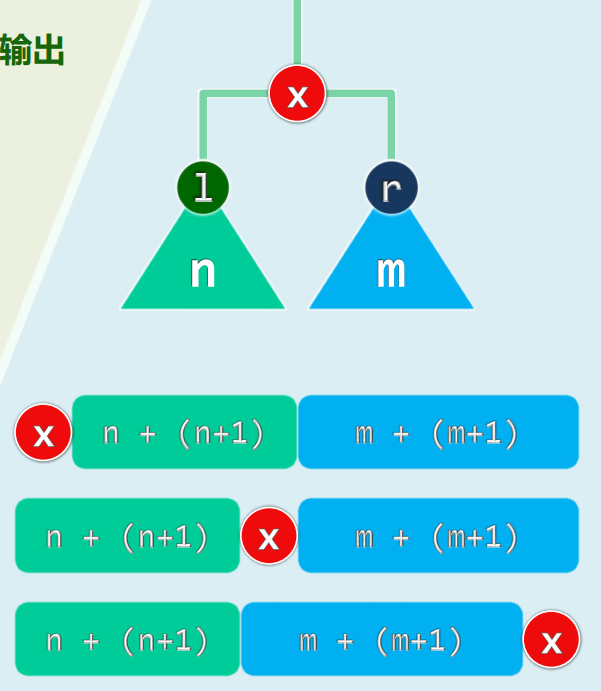
实例:
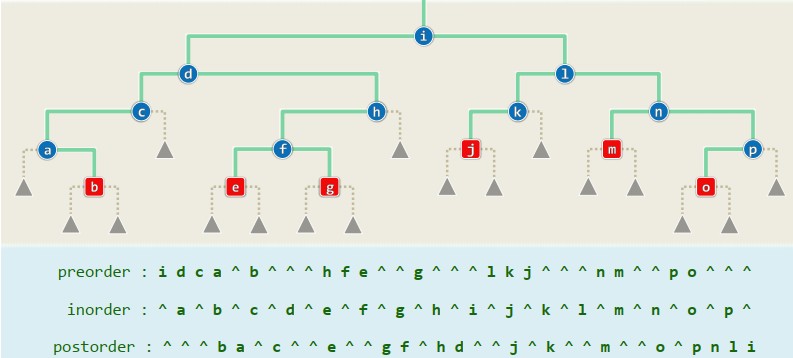
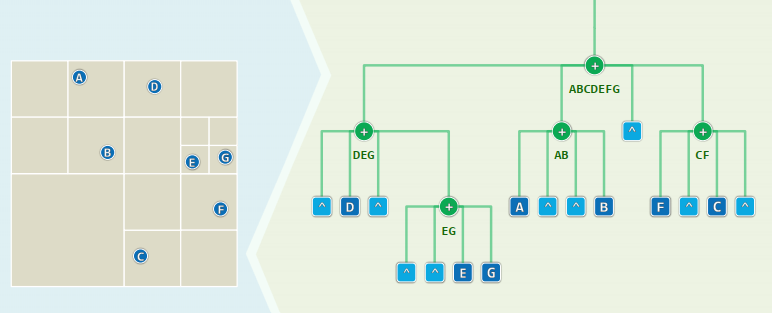
5.3 Huffman编码树
编码
二进制编码
组成数据文件的字符来自字符集
文件的大小取决于:字符的数量 × 各字符编码的长短
通讯带宽有限时,如何对各字符编码使得文件最小?
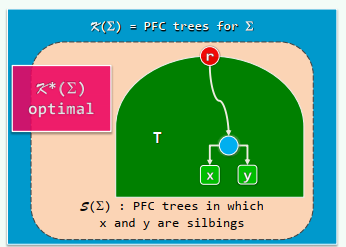
1. PFC编码 (prefix-free code)
将
平均编码长度:
真完全树是最优编码树
2. Huffman编码:最优带权编码树
已知各字符的期望频率,构造最优编码树 频率最高/低的(超)字符,应尽可能放在高/低处 故此,通过适当的交换,同样可以缩短
文件长度正比于平均带圈深度
伪代码:
贪婪策略:频率低的字符优先引入,位置亦更低 为每个字符创建一棵单节点的数,组成森林F,按照出现频率,对数排序 while (F中的树不止一棵) 取出频率最小的两棵树:
和 将它们合并成一棵新树 ,并令: 且 尽管贪心策略未必总能得到最优解,但如上算法的确能够得到最优编码树之一
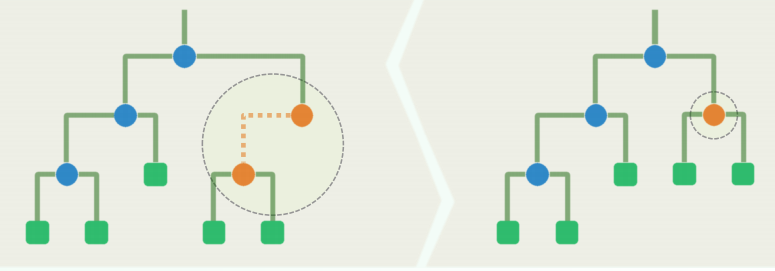
正确性
双子性
最优编码树的特征
首先,每一内部节点都有两个孩子——节点度数均为偶数(0或2),即真二叉树 否则,将1度节点替换为其唯一的孩子,则新书的
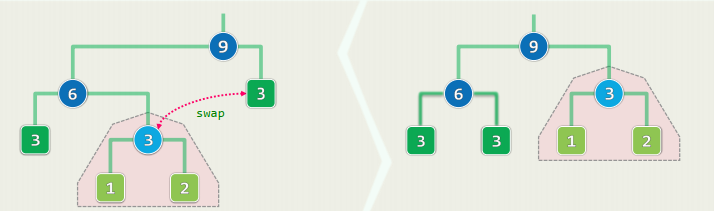
不唯一性
对任一内部节点而言,左右子树互换之后
层次性
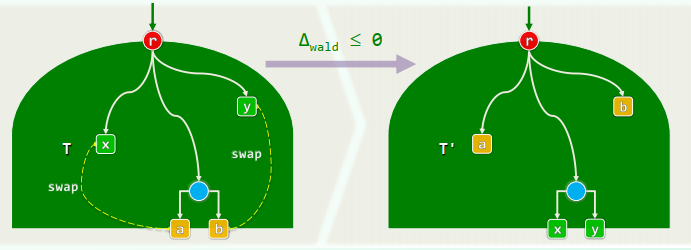
出现频率最低的字符x和y,必在某棵最优编码树中处于最底层,且互为兄弟
否则,任取一棵最优编码树,并在其最底层任取一对兄弟a和b,于是,a和x、b和y 交换之后,
数学归纳和定差
对
定差:对于
因此,只要
3. Huffman编码树:算法实现
Huffman(超)字符
xxxxxxxxxx//仅以可打印字符为例struct HuffChar { char ch; int weight; //字符、频率 HuffChar(char c = '^', int w = 0) : ch(c), weight(w) {}; bool operator< (HuffChar const& hc) { return weight > hc.weight; } bool operator== (HuffChar const& hc) { return weight == hc.weight; } }Huffman(子)树
xxxxxxxxxxusing HuffTree = BinTree<HuffChar>;Huffman森林
xxxxxxxxxxusing HuffForest = List<HuffTree*>;更高效的数据结构实现方式: (得益于已定义的统一接口,支撑Huffman算法的这些底层数据结构可直接彼此替换)
xxxxxxxxxxusing HuffForest = PQ_List<HuffTree*>; //基于列表的优先级队列using HuffForest = PQ_CompHeap<HuffTree*>; //完全二叉堆using HuffForest = PQ_LeftHeap<HuffTree*>; //左式堆构造编码树:
xxxxxxxxxxHuffTree* generateTree(HuffForest * forest) { while (1 < forest->size()) { // 反复迭代,直至森林中仅含一棵树 HuffTree *T1 = minHChar(forest), *T2 = minHChar(forest); HuffTree *S = new HuffTree(); // 创建新树,准备合并T1和T2 S->insert(HuffChar('^', // 根节点权重,取作T1与T2之和 T1->root()->data.weight + T2->root()->data.weight)); S->attach(T1, S->root()); S->attach(S->root(), T2); forest->insertAsLast(S); // T1与T2合并后,重新插回森林 } // assert:循环结束时,森林中唯一的那棵树即是Huffman编码树 return forest->first()->data;}
//查找最小超字符HuffTree* minHChar(HuffForest * forest) { /*如何优化算法*/}构造编码表:
xxxxxxxxxxusing HuffTable = Hashtable<char, char*>; //Huffman编码表static void generateCT // 通过遍历获取各字符的编码 (Bitmap* code, int length, HuffTable* table, BInNodePosi(HuffChar) v) { if (IsLeaf(*v)) //若是叶节点 {table->put(v->data.ch, code->bits2string(length)); return;} if (hasLChild(*v)) //Left = 0,深入遍历 {code->clear(length); generateCT(code, length+1, table, v->lc);} if (HasRChild(*v)) //Right = 1 {code->set(length); generateCT(code, length+1, table, v->rc);}} //总体O(n)优化:向量+列表+优先级队列
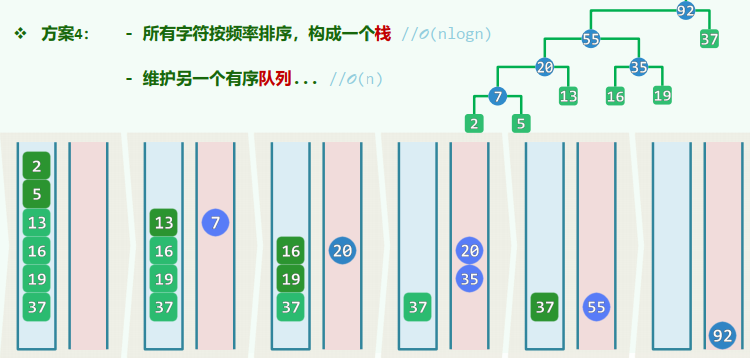
方案1:
初始化时,通过排序得到一个非升序向量: 每次(从后端)取出频率最低的两个节点: 将合并得到的新树插入向量,并保持有序: 方案2:
初始化时,通过排序得到一个非降序列表: 每次(从前端)取出频率最低的两个节点: 将合并得到的新树插入列表,并保持有序: 方案3:
初始化时,将所有数组织为一个优先级队列: 取出频率最低的两个节点,合并得到的新树插入队列: 方案4:
所有字符按频率排序,构成一个栈: 维护另一个有序队列:
5.4 下界:代数判定树
问题P的难度:若问题P存在算法,则所有算法中最低的复杂度成为P的难度
多种角度估算时间、空间复杂度:
最好 / best-case 最坏 / worst-case 平均 / average-case 分摊 / amortized
其中,对最坏情况的估计最保守、最稳妥。因此,首先应考虑最坏情况最优的算法(worst-case optimal)
基于比较的算法(Comparison-Based Algorithm):任何CBD在最坏情况下,都需要
1. 判定树
每个CBA算法都对应于一棵Algebraic Decision Tree 每一可能的输出,都对应于至少一个叶节点 每一次运行过程,都对应于起始于根的某条路径
代数判定树(Algebraic Decision Tree) 针对“比较-判定”式算法的计算模型 给定输入的规模,将所有可能的输入所对应的一系列判断表示出来
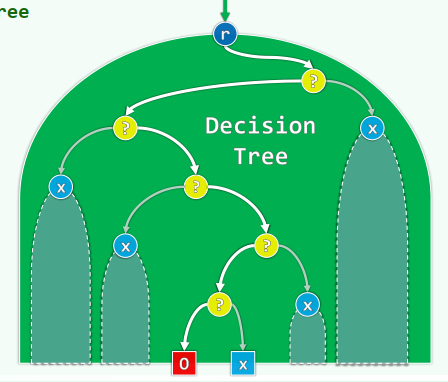
代数判定: 使用某一常数次数代数多项式将任意一组关键码作为变量,对多项式求值 根据结果的符号,确定算法推进方向
叶节点深度 ~ 比较次数 ~ 计算成本 树高 ~ 最坏情况时的计算成本 树高的下界 ~ 所有CBA的时间复杂度下界
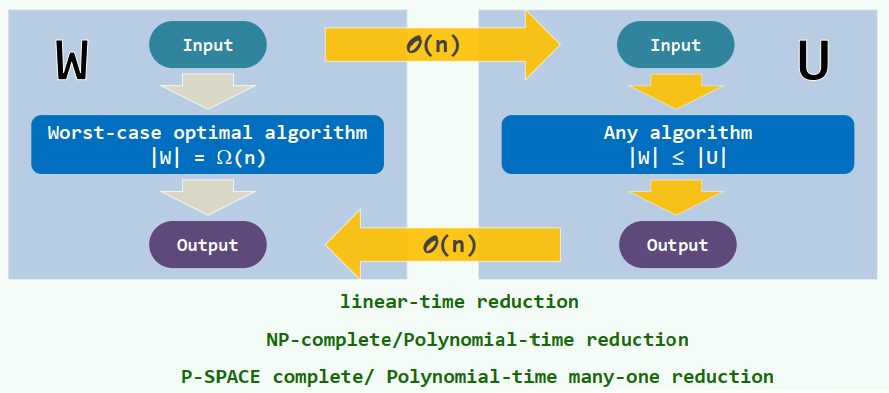
2. 下界:归约
线性归约(Linear-Time Reduction):除了(代数)判定树,归约(reduction)也是确定下界的有利工具
实例:
[Element Uniqueness] 任意n个实数中,是否包含雷同?——
[Integer Element Uniqueness] 任意n个整数中,是否包含雷同?—— [Set Disjointness] 任意一对集合A和B,是否存在公共元素?—— [Red-Blue Matching] 平面上任给n个红色点和n个蓝色点,如何用互不相交的线段配对联结——
5.5 其它应用
Graph/Tree: Diameter / Eccentricity / Radius / Center
Knights of the Round Table / Travelling Knight
6 二叉搜索树 BST
call-by-Key:循关键码访问 数据集中的数据项,统一地表示和实现为词条(entry)形式
xxxxxxxxxxtemplate <typename K, typename V>struct Entry { // 词条模板类 K key; V value; // 关键码、数值 Entry(K k = K(), V v = V()) : key(k), value(v) {}; //默认构造函数 Entry(Entry<K, V> const & e) : key(e.key), value(e.value) {}; bool operator< ( Entry<K, V> const & e ) { return key < e.key; } bool operator> ( Entry<K, V> const & e ) { return key > e.key; } bool operator==( Entry<K, V> const & e ) { return key == e.key; } bool operator!=( Entry<K, V> const & e ) { return key != e.key; } }假设:没有重复关键码
顺序性:任一节点均不小/大于其左/右后代 <==> 任一节点均不小/大于其左/右孩子
顺序性只是对局部特征的刻画,却可导出BST的整体特征
单调性:对树高做数学归纳,可以证明BST的中序遍历序列,必然单调非降
基本接口
xxxxxxxxxxtemplate <typenme T> class BST : public BinTree<T> {public: //以virtual修饰,以便派生类重写 virtual BinNodePosi<T> & search(const T &); //查找 virtual BinNodePosi<T> insert(const T &); //插入 virtual bool remove(const T &); //删除protected: BinNodePosi<T> _hot; //命中节点的父亲 BinNodePosi<T> connect34( //3+4重构,稍晚再详解 BinNodePosi<T>, BinNodePosi<T>, BinNodePosi<T>, BinNodePosi<T>, BinNodePosi<T>, BinNodePosi<T>, BinNodePosi<T>); BinNodePosi<T> rotateAt( BinNodePosi<T> ); //旋转调整}6.1 查找
减而治之:对照中序遍历序列,整个过程可视作有序向量的二分查找
xxxxxxxxxxtemplate <typename T>BinNodePosi<T> & BST<T>::search(const T & e) { if (!_root || e == _root->data) { //空树,或恰好在树根命中 _hot = Null; return _root; } for (_hot = _root; ; ) { BinNodePosi<T> & v = (e < _hot->data) ? _hot->lc : _hot->rc; if (!v || e == v->data) return v; _hot = v; //无论命中或失败,_hot均指向v的父亲(v是根时,hot为NULL) }}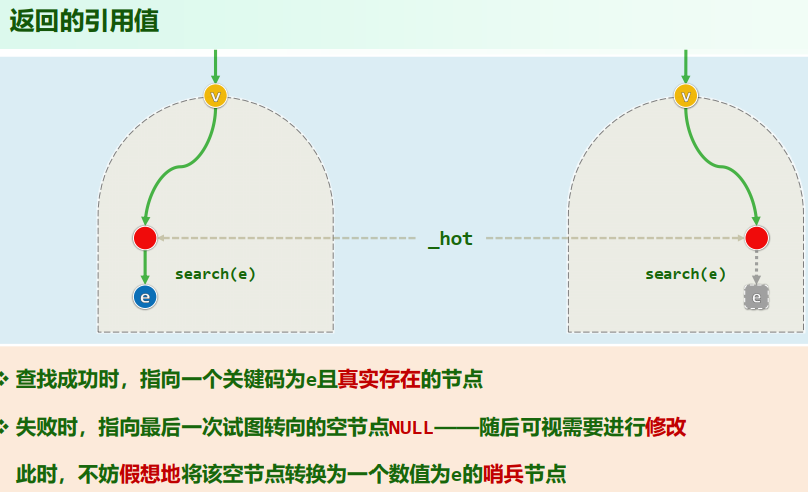
6.2 插入
先借助
search(e)确定插入位置及方向 若不存在,则再将新节点作为叶子插入 _hot为新节点的父亲 v = search(e)为_hot对新孩子的引用 于是,只需令_hot通过v指向新节点
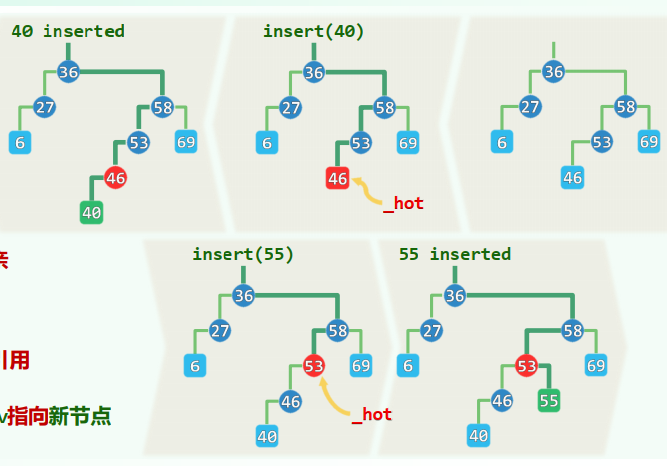
xxxxxxxxxxtemplate <typename T> BinNodePosi<T> BST<T>::insert( const T & e ) { BinNodePosi<T> & x = search( e ); //查找目标(留意_hot的设置) if ( ! x ) { //既禁止雷同元素,故仅在查找失败时才实施插入操作 x = new BinNode<T>( e, _hot ); //在x处创建新节点,以_hot为父亲 _size++; updateHeightAbove( x ); //更新全树规模,更新x及其历代祖先的高度 } return x; //无论e是否存在于原树中,至此总有x->data == e} //时间主要消耗于search(e)和updateHeightAbove(x);均线性正比于x的深度,不超过树高6.3 删除
xxxxxxxxxxtemplate <typename T> bool BST<T>::remove( const T & e ) { BinNodePosi<T> & x = search( e ); //定位目标节点 if ( !x ) return false; //确认目标存在(此时_hot为x的父亲) removeAt( x, _hot ); //分两大类情况实施删除,更新全树规模 _size--; //更新全树规模 updateHeightAbove( _hot ); //更新_hot及其历代祖先的高度 return true;} //累计O(h)时间:search()、updateHeightAbove();还有removeAt()中可能调用的succ()
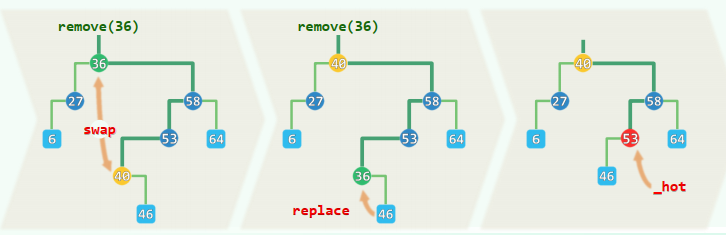
template <typename T>static BinNodePosi<T> removeAt(BinNodePosi<T> & x, BinNodePosi<T> & hot) { BinNodePosi<T> w = x; //实际被摘除的节点,初值同x BinNodePosi<T> succ = NULL; //实际被删除节点的接替者 if ( !HasLChild( *x ) ) succ = x = x->rc; //左子树为空 else if ( ! HasRChild( *x ) ) succ = x = x->lc; //右子树为空 else { w = w->succ(); swap( x->data, w->data ); //令*x与其后继*w互换数据 BinNodePosi<T> u = w->parent; //原问题即转化为,摘除非二度的节点w ( u == x ? u->rc : u->lc ) = succ = w->rc; //兼顾特殊情况:u可能就是x } hot = w->parent; //记录实际被删除节点的父亲 if ( succ ) succ->parent = hot; //将被删除节点的接替者与hot相联 release( w->data ); release( w ); return succ; //释放被摘除节点,返回接替者} //此类情况仅需O(1)时间主要难点:双分支情况下的删除
调用
BinNode::succ()找到的直接后继(必无左孩子),交换 进而问题转换为删除 ,可按前一情况处理 尽管顺序性在中途曾一度不合,但最终必将重新恢复
6.4 平衡 BBST
1. 期望树高
BST的主要接口
search()、insert()和remove()的运行时间在最坏情况下,均线性正比于其高度在最坏情况下,二叉搜索树可能彻底退化为列表 下面给出此类较坏情况下的概率分析
随机生成:n个词条按随机排列一次插入
设各排列出现的概率均等(
remove(),也可通过随机使用succ()和pred(),避免逐渐倾侧的趋势随机组成:n个互异节点,在遵守顺序性的前提下,随机确定拓扑连接关系
由n个互异节点随机组成的BST,若共计
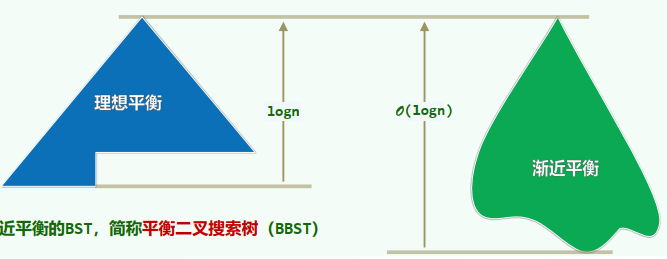
2. 理想与渐进平衡
理想平衡:由
大致相当于完全树甚至满树:叶节点只能出现与最底部的两层——条件过于苛刻
渐近平衡:高度渐近地不超过
渐进平衡的BST,简称平衡二叉搜索树
3. 等价变换
- 上下可变:连接关系不尽相同,承袭关系可能颠倒
- 左右不乱:中序遍历序列完全一致,全局单调非降
各种BBST都可视作BST的某一子集,相应地满足精心设计的限制条件
单次动态修改操作后,至多
处局部不再满足限制条件(可能相继违反,未必同时) 可在 时间内,使局部重新满足
等价变换 + 旋转调整
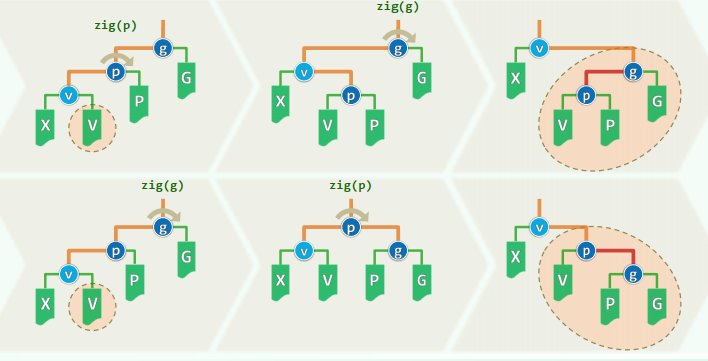
刚刚失衡的BST,必可迅速转换为一棵等价的BBST——为此,只需
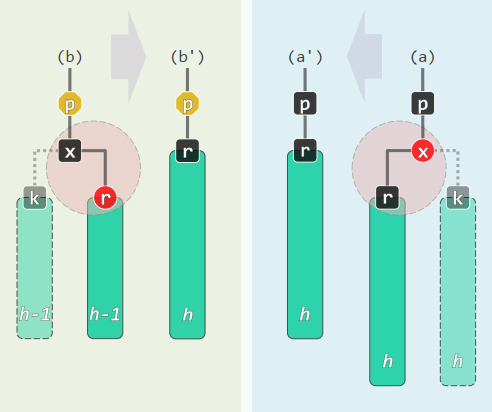
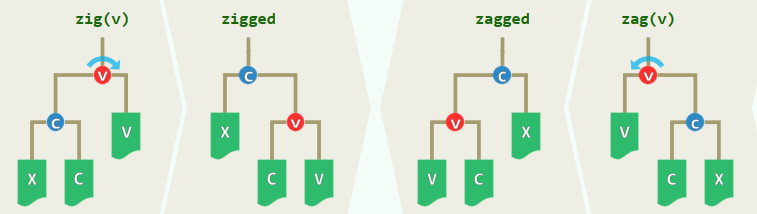
zig和zag:仅涉及常数个节点,只需调整其间的连接关系,均属于局部的基本操作 调整之后:v/c深度加/减1,子(全)树高度的变化幅度,上下差异不超过1 实际上,经过不超过
6.5 AVL树
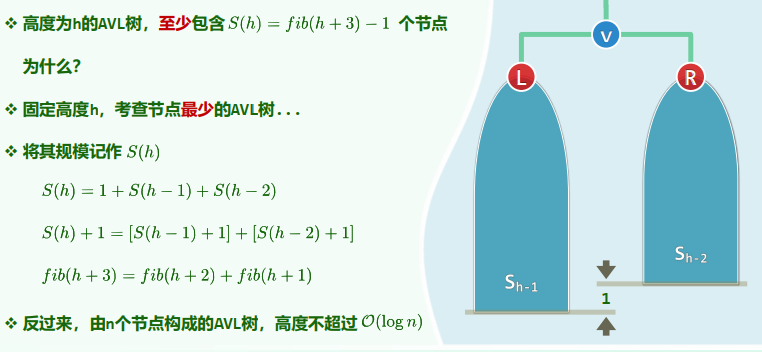
平衡因子Balance Factor:
AVL树未必理想平衡,但必然渐近平衡
渐近平衡
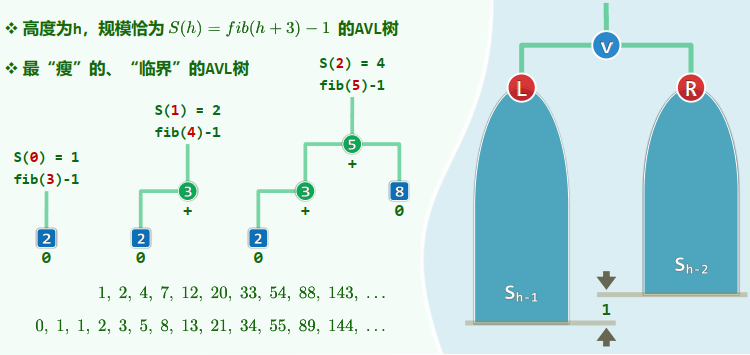
高度为h的AVL树,至少包含
个节点
重平衡
失衡
插入:从祖父开始,每个祖先都有可能失衡,且可能同时失衡,但只需调整一次 删除:从父亲开始,每个祖先都有可能失衡,且至多一个,但可能需要调整多次
重平衡
局部性:所有旋转都在局部进行 //每次只需
时间 快速性:在每一深度只需检查并旋转至多一次 //共 次
xxxxxxxxxx//理想平衡//平衡因子//AVL平衡条件
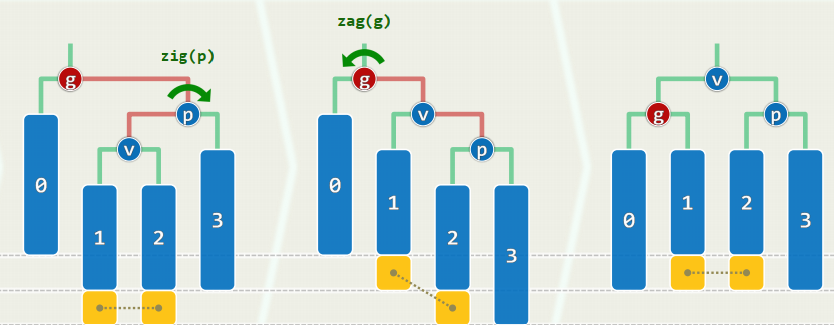
template <typename T> class AVL : public BST<T> { //由BST派生public: //BST::search()等接口,可直接沿用 BinNodePosi<T> insert( const T & ); //插入(重写) bool remove( const T & ); //删除(重写)};1. 插入
同时可有多个失衡节点,最低者g不低于x的祖先 g经单旋调整后复衡,子树高度复原 更高祖先也必平衡,全树复衡
单旋:黄色方块恰好存在其一
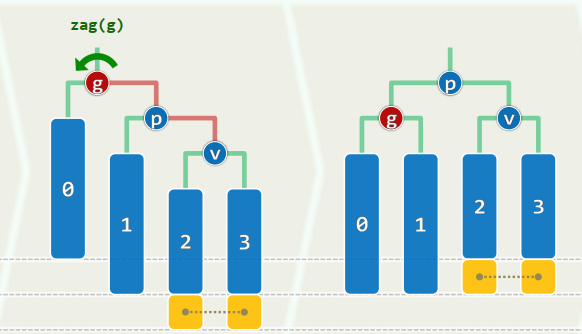
双旋
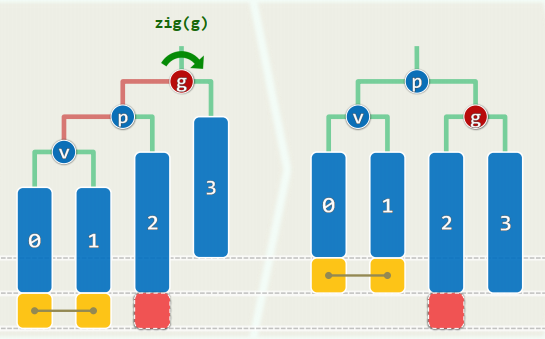
xxxxxxxxxxtemplate <typename T> BinNodePosi<T> AVL<T>::insert( const T & e ) { BinNodePosi<T> & x = search( e ); if ( x ) return x; //若目标尚不存在 BinNodePosi<T> xx = x = new BinNode<T>( e, _hot ); _size++; //则创建新节点 // 此时,若x的父亲_hot增高,则祖父有可能失衡 for ( BinNodePosi<T> g = _hot; g; g = g->parent ) //从_hot起,逐层检查各代祖先g if ( ! AvlBalanced( *g ) ) { //一旦发现g失衡,则通过调整恢复平衡 FromParentTo(*g) = rotateAt(tallerChild(tallerChild(g))); break; //局部子树复衡后,高度必然复原;其祖先亦必如此,故调整结束 } else //否则(g仍平衡) updateHeight(g); //只需更新其高度(即便g未失衡,高度亦可能增加) return xx; //返回新节点位置}2. 删除
同时至多一个失衡节点g,首个可能就是x的父亲_hot 复衡后子树高度未必复原,更高祖先仍可能随之失衡 失衡可能持续向上传播,最多需做
次调整
单旋:黄色方块至少存在其一,红色方块可有可无
双旋
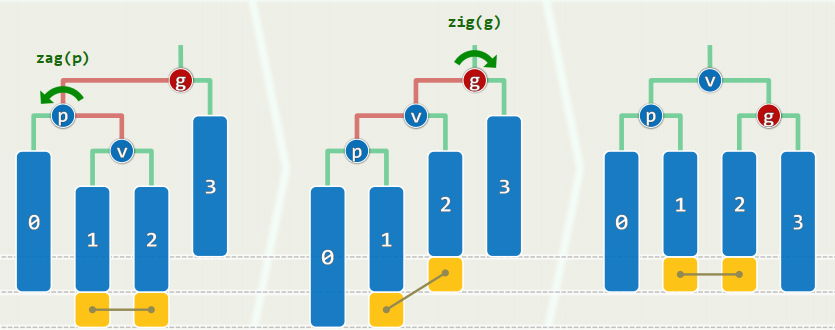
xxxxxxxxxxtemplate <typename T> bool AVL<T>::remove( const T & e ) { BinNodePosi<T> & x = search( e ); if ( !x ) return false; //若目标的确存在 removeAt( x, _hot ); _size--; //则在按BST规则删除之后, _hot及祖先均有可能失衡 // 以下,从_hot出发逐层向上,依次检查各代祖先g for ( BinNodePosi<T> g = _hot; g; g = g->parent ) { if ( !AvlBalanced(*g) ) //一旦发现g失衡,则通过调整恢复平衡 g = FromParentTo(*g) = rotateAt(tallerChild(tallerChild(g))); updateHeight(g); //更新高度(注意:即便g未曾失衡或已恢复平衡,高度均可能降低) } //可能需做过O(logn)次调整;无论是否做过调整,全树高度均可能下降 return true; //删除成功}3. (3+4)-重构
设g为最低的失衡节点,沿最长分支考察祖孙三代:g~p~v,按中序遍历次序,重命名为:a < b < c 它们总共拥有四个子树(或为空),按中序遍历次序,重命名为:T0 < T1 < T2 < T3 将原先以g为根的子树S,替换为一棵新子树S` 等价变换,保持中序遍历次序:T0 < a < T1 < b < T2 < c < T3
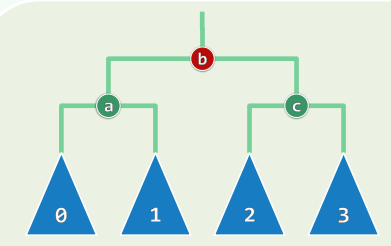
xxxxxxxxxxtemplate <typename T> BinNodePosi<T> BST<T>::connect34(BinNodePosi<T> a, BinNodePosi<T> b, BinNodePosi<T> c, BinNodePosi<T> T0, BinNodePosi<T> T1, BinNodePosi<T> T2, BinNodePosi<T> T3) { a->lc = T0; if (T0) T0->parent = a; a->rc = T1; if (T1) T1->parent = a; c->lc = T2; if (T2) T2->parent = c; c->rc = T3; if (T3) T3->parent = c; b->lc = a; a->parent = b; b->rc = c; c->parent = b; updateHeight(a); updateHeight(c); updateHeight(b); return b;}统一调整:
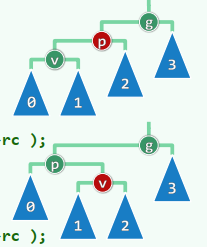
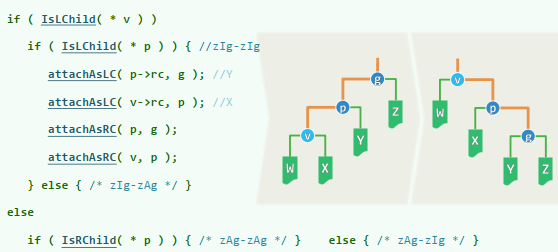
xxxxxxxxxxtemplate <typename T> BinNodePosi<T> BST<T>::rotateAt( BinNodePosi<T> v ) { BinNodePosi<T> p = v->parent, g = p->parent; if ( IsLChild( * p ) ) //zig if ( IsLChild( * v ) ) { //zig-zig p->parent = g->parent; //向上联接 return connect34( v, p, g, v->lc, v->rc, p->rc, g->rc ); } else { //zig-zag v->parent = g->parent; //向上联接 return connect34( p, v, g, p->lc, v->lc, v->rc, g->rc ); } else { /*.. zag-zig & zag-zag ..*/ }}AVL:综合评价
优点:
无论查找、插入或删除,最坏情况下的复杂度均为
7 BST Application
Range Query
Counting and Reporting
1D Range Query
Binary Search + enumerating:
2D Planar Range Query
Inclusion-Exclusion Principle: query
disjoint subtrees
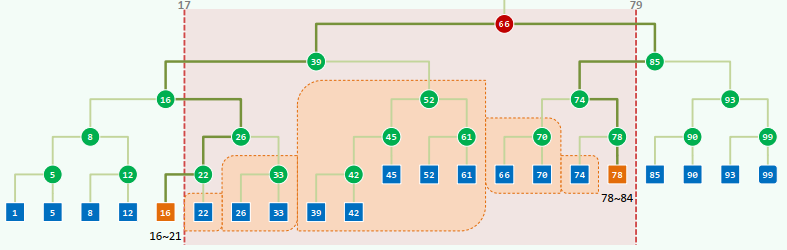
1. kd-Tree: 1D
结构:a complete (balanced) BST
search(x): return the MAXIMUM key not greater than x
disjoint subtrees
Starting from the LCA (lowest common ancestor), traverse path(16) and path(78) once more resp. All R/L-turns along path(16)/path(78) are ignored and the R/L subtree at each L/R-turn is reported
Complexity: Query:
Preprocessing: Storage:
2. kd-Tree: 2D
To extend the BBST method to planar GRS, we - divide the plane recursively and - arrange the regions into a kd-tree
Definition: each region is defined to be open/closed on the left-lower/right-upper sides
Example:
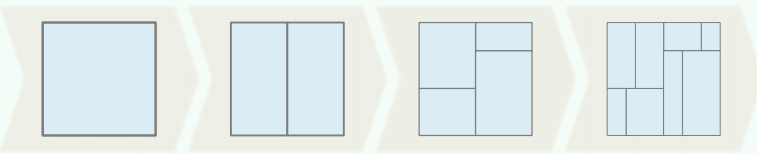
Quadtree
buildKdTree(P, d)
这个实现方式不是很好,参考PA3-5
xxxxxxxxxx// construct a 2d-(sub)tree for point (sub)set P at depth dif ( P == {p} ) return CreateLeaf( p ) //baseroot = CreateKdNode()root->splitDirection = Even(d) ? VERTICAL : HORIZONTALroot->splitLine = FindMedian( root->splitDirection, P ) //O(n)!( P1, P2 ) = Divide( P, root->splitDirection, root->splitLine ) //DACroot->lc = buildKdTree( P1, d + 1 ) //recurseroot->rc = buildKdTree( P2, d + 1 ) //recursereturn( root )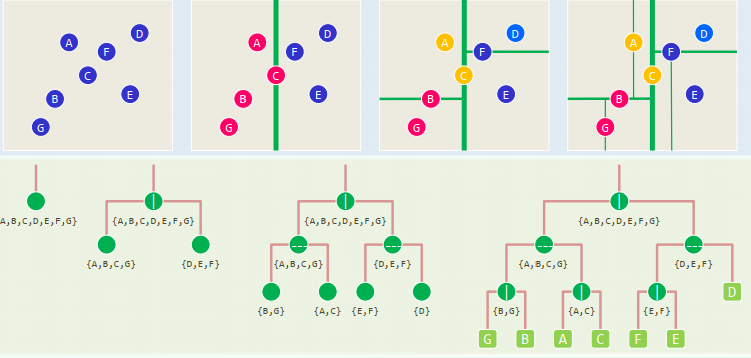
each node => each rectangular sub-region of the plane each of these subsets is called a canonical subset for each internal node X with children L and R,
sub-regions of nodes at a same depth never intersect with each other and their union covers the entire plane
Query
xxxxxxxxxxif ( isLeaf( v ) )if ( inside( v, R ) ) report(v)returnif ( region( v->lc ) ⊆ R )reportSubtree( v->lc )else if ( region( v->lc ) ∩ R ≠ Φ)kdSearch( v->lc, R )if ( region( v->rc ) ⊆ R )reportSubtree( v->rc )else if ( region( v->rc ) ∩ R ≠ Φ)kdSearch( v->rc, R )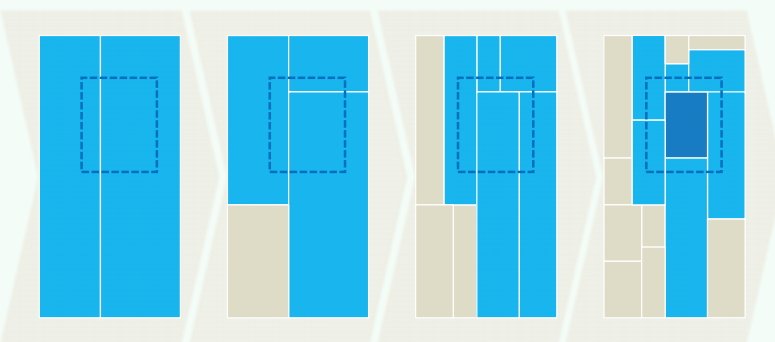
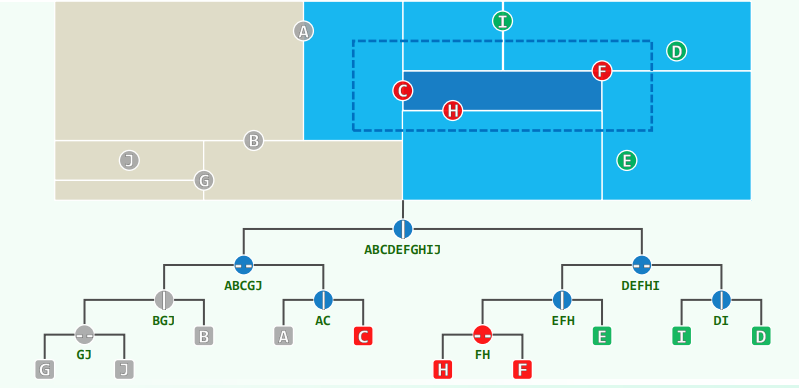
3. Complexity
Preprocessing
Storage the tree has a height of
Query Time

beyond 2D:
Multi-Level Search Tree
2D Range Query = x-Query * y-Query

Complexity:
Query Time =
2-level search tree: build-tree in
time each input point is stored in y-trees needs space x-range query needs
time to locate the nodes then for each of these nodes, a y-range search is invoked, which needs time
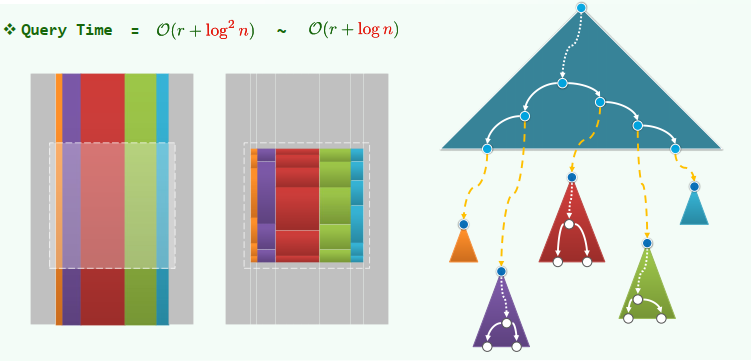
Query Algorithm
Determine the canonical subsets of points that satisfy the first query. Find out from each canonical subset which points lie within the y-range.
Beyond 2D: a d-level tree for S uses
storage can be constructed in time each orthogonal range query of S can be answered in time
Range Tree
Interval Tree
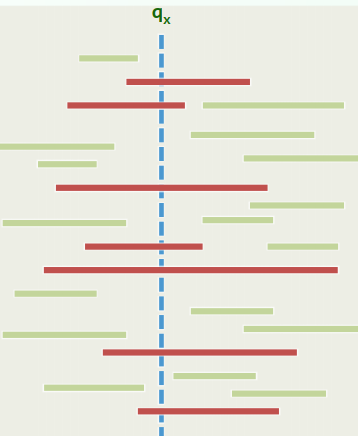
Stabbing Query:
Given a set of intervals in general position on the x-axis:
and a query point Find all intervals that contain :
1. Partitioning
Median: Let
be the set of all endpoints Let be the median of
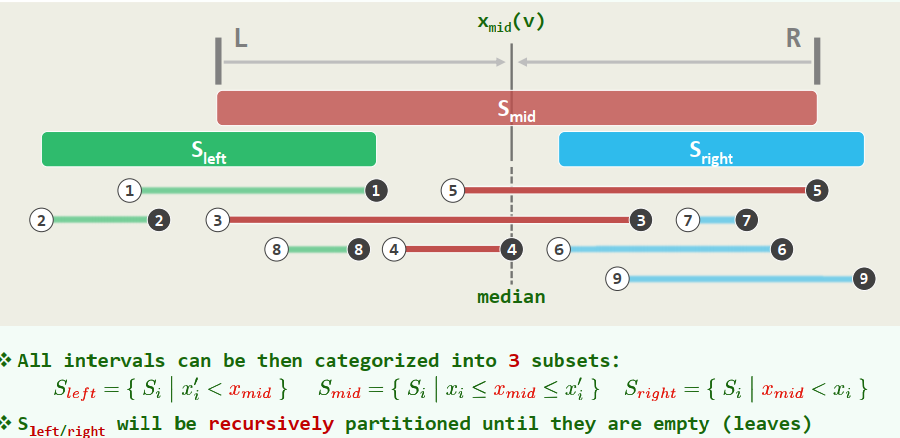
Best case: Worst case:
2. Construction
Complexity:
Hint: avoid repeatedly sorting
each segment appears twice (one in each list)
3. queryIntervalTree
xxxxxxxxxxif (!v) return; //baseif ( q_x < x_mid(v) ) report all segments of S_mid(v) containing q_x; queryIntervalTree( lc(v), q_x );else if ( x_mid(v) < q_x ) report all segments of S_mid(v) containing q_x; //(优化)preprocessing: 对右端点进行排序 queryIntervalTree( rc(v), q_x );else //with a probability ≈ 0 report all segments of S_mid( v ); //both rc(v) & lc(v) can be ignored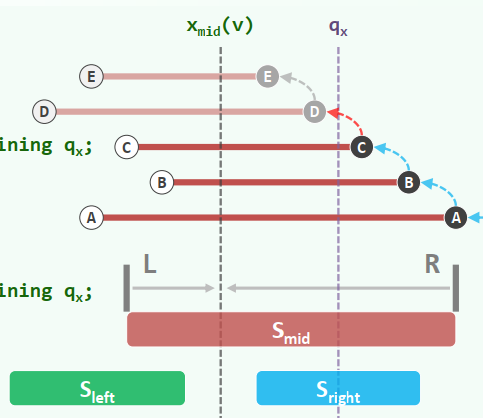
Query Time:
Segment Tree
Stabbing Query
Discretization 离散化
Let
be n intervals on the x-axis sort all the endpoints into elementary intervals are hence defined as:

Worst Case: every interval spans
EI's and a total space of is required
Sorted Vector --> BBST
For each leaf
, denote the corresponding elementary interval as //range of domination denote the subset of intervals spanning as and store at To find all intervals containing
, we can find the leaf whose contains // time for a BBST and then report // time
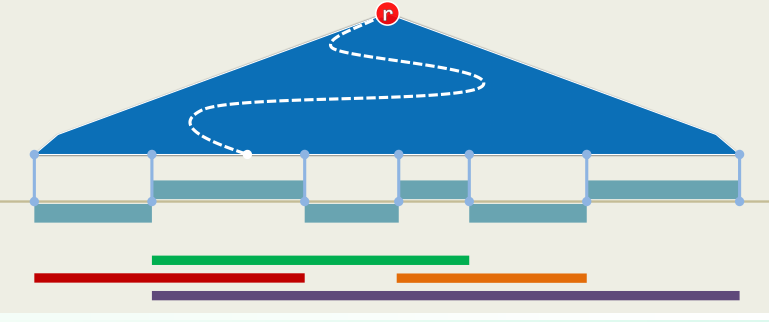
Store each interval at
Canonical Subsets with
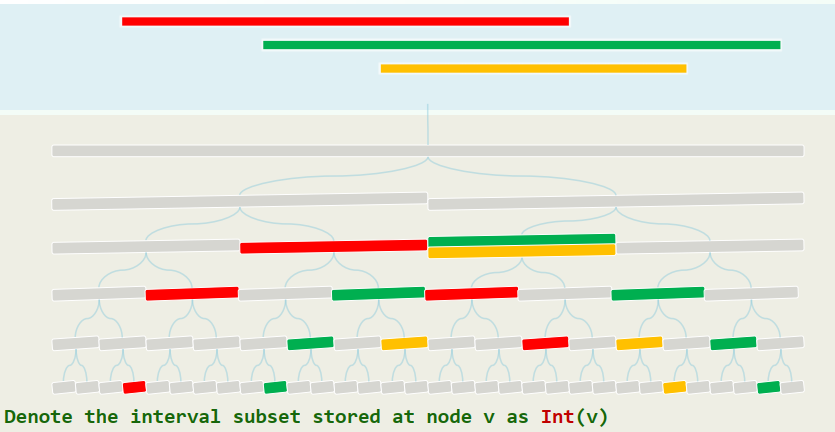
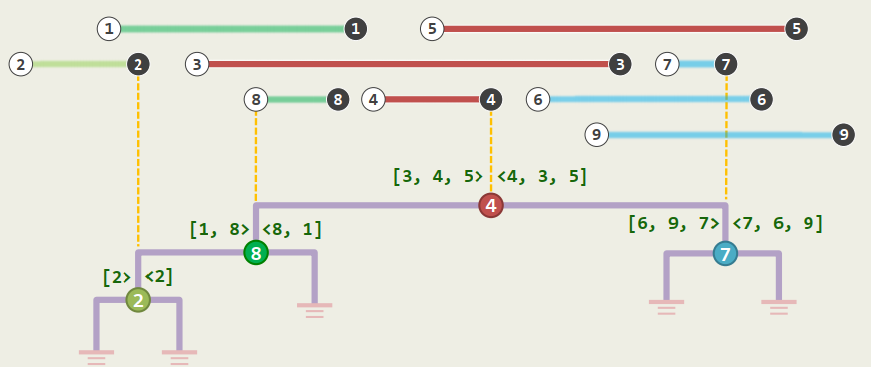
1. BuildSegementTree
Sort all endpoints in
before determining all the EI's: Create a on all the EI's: Determine for each node : if done in a bottom-up manner For each of , InsertSegment( T.root, s )
xxxxxxxxxx//InsertSegment(v, s)if ( R(v) ⊆ s ) //greedy by top-down store s at v and return;if ( R( lc(v) ) ∩ s ≠ Φ ) //recurse InsertSegment( lc(v), s );if ( R( rc(v) ) ∩ s ≠ Φ ) //recurse InsertSegment( rc(v), s );
At each level, ≤ 4 nodes are visited (2 stores + 2 recursions)// O(logn) time2. Query
xxxxxxxxxx//Query(v, q_x)report all the intervals in Int(v)if ( v is a leaf ) returnif ( qx ∈ Int( lc(v) ) ) Query( lc(v), qx )else Query( rc(v), qx )Complexity:
Only one node is visited per level, altogether nodes At each node the CS is reported in time: Reporting all the intervals: costs time
3. Conlusion
a segment tree of size:
8 高级搜索树
存储器现状
CPU Register: [cycles] = 0, [sec] = ns SRAM/cache: [cycles] = 4~75, [sec] = ns DRAM/main memory: [cycles] = 102, [sec] = ns DISK: [cycles] = 107, [sec] = ms
不同类型的存储器,容量、访问速度差异悬殊 实际运行时间主要取决于:相邻存储级别之间数据传输(I/O)的速度与次数
Definition(内存 / 外存):所有相对于当前存储器级别更低的都叫做“外存”,反之称为“内存”
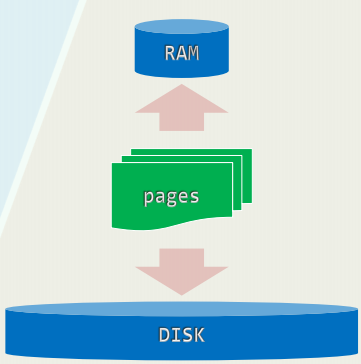
分级存储:批量访问 以页(page)或块(block)为单位,借助缓冲区,可大大缩短字节的平均访问时间
xxxxxxxxxx//缓冲区默认容量int setvbuf ( //定制缓冲区FILE* fp, //流char* buf, //缓冲区int _Mode, //_IOFBF | _IFLBF | _IONBFsize_t size); //缓冲区容量int fflush(FILE* fp); //强制清空缓冲区
8.1 B树
基本结构
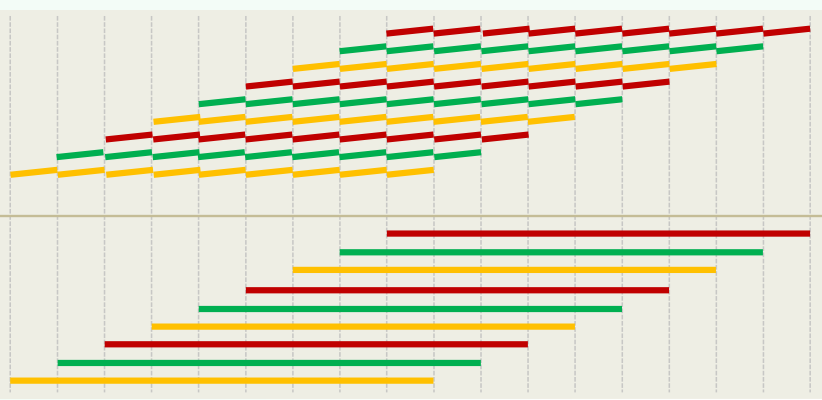
每d代合并为超级节点,
I/O优化:多级存储系统中使用B树,可针对外部查找,大大减少I/O次数 普通AVL:若有
个记录,每次查找需要 次I/O操作 B树:充分利用外存的批量访问,每下降一层,都以超级节点为单位,读入一组关键码 目前多数数据库系统采用 。取 ,则每次查找只需要 次I/O
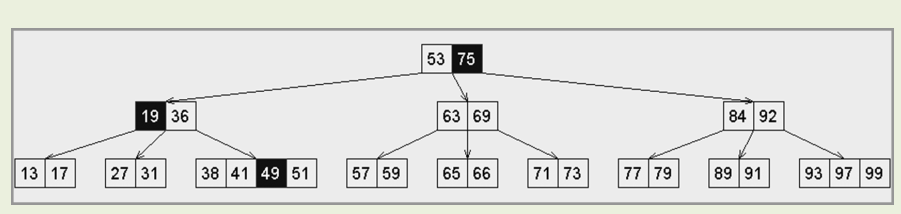
各节点的分支数,可能是2,3或4 各节点所含key的数目,可能是1,2或3
xxxxxxxxxx//BTNodetemplate <typename T> struct BTNode { //B-树节点 BTNodePosi<T> parent; //父 Vector<T> key; //关键码(总比孩子少一个) Vector< BTNodePosi<T> > child; //孩子 BTNode() { parent = NULL; child.insert( NULL ); } BTNode( T e, BTNodePosi<T> lc = NULL, BTNodePosi<T> rc = NULL ) { parent = NULL; //作为根节点 key.insert( e ); //仅一个关键码,以及 child.insert( lc ); if ( lc ) lc->parent = this; //左孩子 child.insert( rc ); if ( rc ) rc->parent = this; //右孩子 }};//BTreetemplate <typename T> using BTNodePosi = BTNode<T>*; //B-树节点位置template <typename T> class BTree { //B-树protected: int _size; int _m; BTNodePosi<T> _root; //关键码总数、阶次、根 BTNodePosi<T> _hot; //search()最后访问的非空节点位置 void solveOverflow( BTNodePosi<T> ); //因插入而上溢后的分裂处理 void solveUnderflow( BTNodePosi<T> ); //因删除而下溢后的合并处理public: BTNodePosi<T> search( const T & e ); //查找 bool insert( const T & e ); //插入 bool remove( const T & e ); //删除};1. 查找
xxxxxxxxxxtemplate <typename T> BTNodePosi<T> BTree<T>::search( const T & e ) { BTNodePosi<T> v = _root; _hot = NULL; //从根节点出发 while ( v ) { //逐层深入地 Rank r = v->key.search( e ); //在当前节点对应的向量中顺序查找 if ( 0 <= r && e == v->key[r] ) return v; //若成功,则返回;否则... _hot = v; v = v->child[ r + 1 ]; //沿引用转至对应的下层子树,并载入其根(I/O) } //若因!v而退出,则意味着抵达外部节点 return NULL; //失败}最大树高:含
推导:
取 ,树高约降低至 ~
2. 插入
xxxxxxxxxxtemplate <typename T> bool BTree<T>::insert( const T & e ) { BTNodePosi<T> v = search( e ); if ( v ) return false; //确认e不存在 Rank r = _hot->key.search( e ); //在节点_hot中确定插入位置 _hot->key.insert( r+1, e ); //将新关键码插至对应的位置 _hot->child.insert( r+2, NULL ); _size++; //创建一个空子树指针 solveOverflow( _hot ); //若上溢,则分裂 return true; //插入成功}分裂:关键码上升一层,并分裂以所得的两个节点为左右孩子
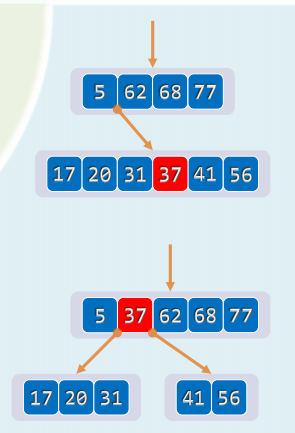
再分裂:若上溢节点的父亲本就饱和,则在接纳被提升的关键码之后也将上溢,逐层向上传播,总体执行时间正比于分裂次数
分裂至根节点:B树高度增加,且新生的树根仅有两个分支
xxxxxxxxxx//上溢修复template <typename T> void BTree<T>::solveOverflow( BTNodePosi<T> v ) { while ( _m <= v->key.size() ) { //除非当前节点不再上溢 Rank s = _m / 2; //轴点(此时_m = key.size() = child.size() - 1) BTNodePosi<T> u = new BTNode<T>(); //注意:新节点已有一个空孩子 for ( Rank j = 0; j < _m - s - 1; j++ ) { //分裂出右侧节点u(效率低可改进) u->child.insert( j, v->child.remove( s + 1 ) ); //v右侧_m–s-1个孩子 u->key.insert( j, v->key.remove( s + 1 ) ); //v右侧_m–s-1个关键码 } u->child[ _m - s - 1 ] = v->child.remove( s + 1 ); if ( u->child[ 0 ] ) //若u的孩子们非空,则统一令其以u为父节点 for ( Rank j = 0; j < _m - s; j++ ) u->child[ j ]->parent = u; BTNodePosi<T> p = v->parent; //v当前的父节点p if ( ! p ) { //若p为空,则创建之(全树长高一层,新根节点恰好两度) _root = p = new BTNode<T>(); p->child[0] = v; v->parent = p; } Rank r = 1 + p->key.search( v->key[0] ); //p中指向u的指针的秩 p->key.insert( r, v->key.remove( s ) ); //轴点关键码上升 p->child.insert( r + 1, u ); u->parent = p; //新节点u与父节点p互联 v = p; //上升一层,如有必要则继续分裂——至多O(logn)层 } //while} //solveOverflow3. 删除
xxxxxxxxxx//确保目标在叶子中template <typename T>bool BTree<T>::remove( const T & e ) { BTNodePosi<T> v = search( e ); if ( ! v ) return false; //确认e存在 Rank r = v->key.search(e); //e在v中的秩 if ( v->child[0] ) { // 若v非叶子,则 BTNodePosi<T> u = v->child[r + 1]; //在右子树中 while ( u->child[0] ) u = u->child[0]; //一直向左,即可找到e的后继(必在底层) v->key[r] = u->key[0]; v = u; r = 0; } //assert: 至此, v必位于最底层,且其中第r个关键码就是待删除者 v->key.remove( r ); v->child.remove( r + 1 ); _size--; solveUnderflow( v ); return true; //如有必要,需做旋转或合并}
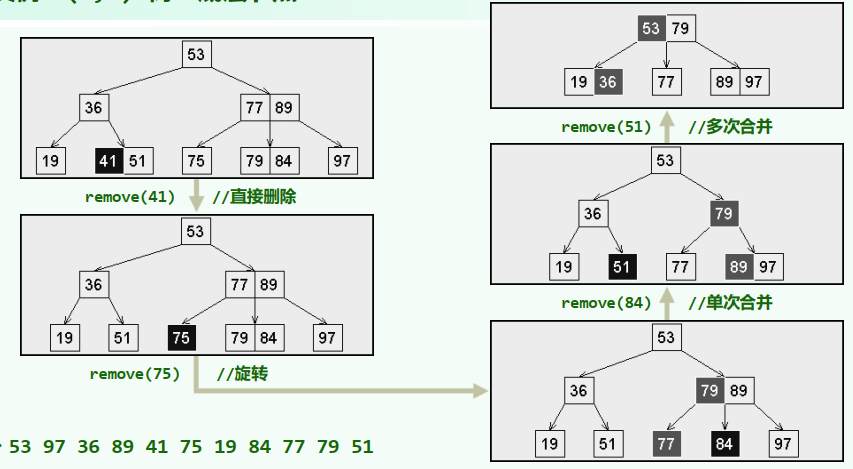
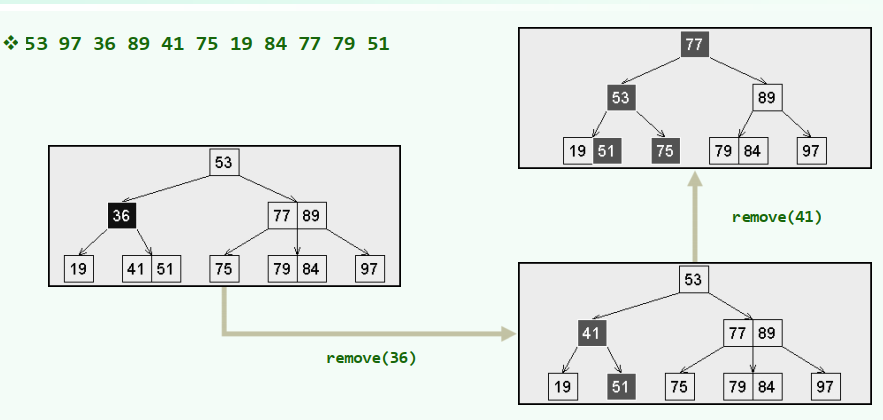
-树:底层节点
-树:非底层节点
代码实现:

思考:B树的插入删除优先策略非对称(插入:split,删除:rotate 而不是 merge)
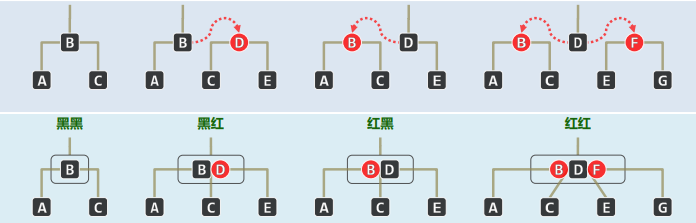
8.2 红黑树 Red-Black Tree
并发性 Concurrent Access To A Database: 修改之前先加锁(lock);完成后解锁(unlock) 访问延迟主要取决于“lock/unlock”周期 对于BST而言,每次修改过程中,唯结构有变(reconstruction)处才需加锁 访问延迟主要取决于这类局部之数量 Red-Black Tree保证无论insert / remove,结构变化均不超过
持久性 Persistent Structures:支持对历史版本的访问 Partial Persistence:仅支持对历史版本的读取 每个版本的新增复杂度,仅为
,甚至 ...!
1. 结构
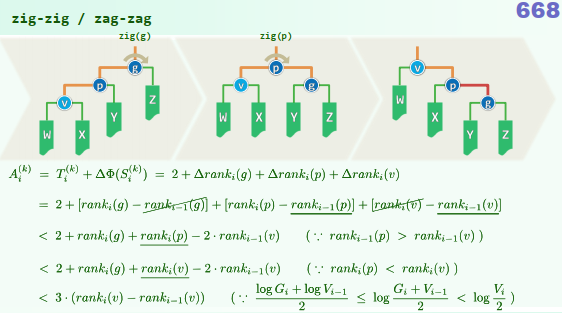
由红、黑两类节点组成的BST,统一增设外部节点NULL,使之成为真二叉树
规则:
- 树根:必为黑色
- 外部节点:均为黑色
- 红节点:只能有黑孩子(及黑父亲)
- 外部节点:黑深度(黑的真祖先数目)相等 亦即根(全树)的黑高度 子树的黑高度,即后代NULL的相对黑深度
(一种直观理解方式:)
于是,每棵红黑树都对应于一棵(2,4)-树:将黑节点与其红孩子视作关键码,再合并为B-树的超级节点(无非四种组合)
红黑树
- 包含
- 若
xxxxxxxxxxtemplate <typename T> class RedBlack : public BST<T> { //红黑树public: //BST::search()等其余接口可直接沿用 BinNodePosi<T> insert( const T & e ); //插入(重写) bool remove( const T & e ); //删除(重写)protected: void solveDoubleRed( BinNodePosi<T> x ); //双红修正 void solveDoubleBlack( BinNodePosi<T> x ); //双黑修正 int updateHeight( BinNodePosi<T> x ); //更新节点x的高度(重写)};
template <typename T> int RedBlack<T>::updateHeight( BinNodePosi<T> x ) { return x->height = IsBlack( x ) + max( stature( x->lc ), stature( x->rc ) ); }2. 插入
首先按照BST规则插入关键码
,首先将 染红,可能违反规则3:双红 (double-red) 考察:祖父 g = p->parent和叔父u = uncle(x) = sibling(p)
xxxxxxxxxxtemplate <typename T> BinNodePosi<T> RedBlack<T>::insert( const T & e ) { // 确认目标节点不存在(留意对_hot的设置) BinNodePosi<T> & x = search( e ); if ( x ) return x; // 创建红节点x,以_hot为父,黑高度 = 0 x = new BinNode<T>( e, _hot, NULL, NULL, 0 ); _size++; // 如有必要,需做双红修正,再返回插入的节点 BinNodePosi<T> xOld = x; solveDoubleRed( x ); return xOld;} //无论原树中是否存有e,返回时总有x->data == e
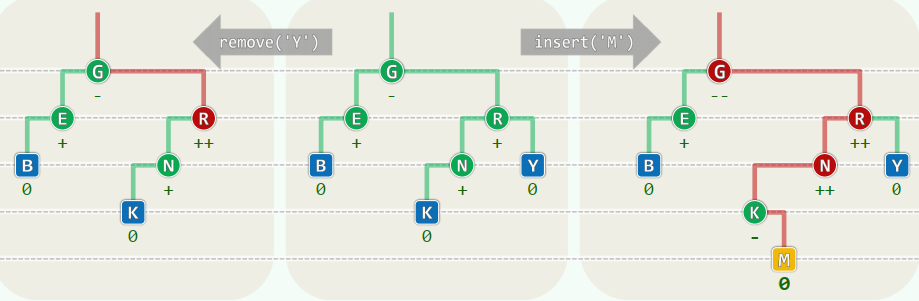
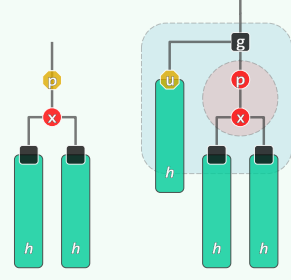
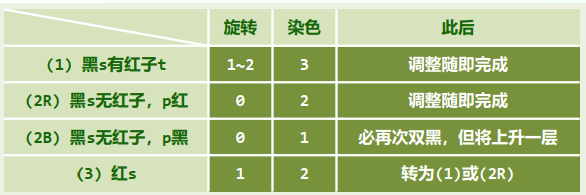
template <typename T> void RedBlack<T>::solveDoubleRed( BinNodePosi<T> x ) { if ( IsRoot( *x ) ) //若已(递归)转至树根,则将其转黑,整树黑高度也随之递增 { _root->color = RB_BLACK; _root->height++; return; } //否则... BinNodePosi<T> p = x->parent; //考查x的父亲p(必存在) if ( IsBlack( p ) ) return; //若p为黑, 则可终止调整;否则 BinNodePosi<T> g = p->parent; //x祖父g必存在,且必黑 BinNodePosi<T> u = uncle( x ); //以下视叔父u的颜色分别处理 if ( IsBlack( u ) ) { //u为黑(或NULL) // 若x与p同侧,则p由红转黑,x保持红;否则,x由红转黑,p保持红 if ( IsLChild( *x ) == IsLChild( *p ) ) p->color = RB_BLACK; else x->color = RB_BLACK; g->color = RB_RED; //g必定由黑转红 BinNodePosi<T> gg = g->parent; //great-grand parent BinNodePosi<T> r = FromParentTo( *g ) = rotateAt( x ); r->parent = gg; //调整之后的新子树,需与原曾祖父联接 } else { //u为红 p->color = RB_BLACK; p->height++; //p由红转黑,增高 u->color = RB_BLACK; u->height++; //u由红转黑,增高 g->color = RB_RED; //在B-树中g相当于上交给父节点的关键码,故暂标记为红 solveDoubleRed( g ); //继续调整:若已至树根,接下来的递归会将g转黑(尾递归) }}RR-1:u->color == B 此时,
x,p,g的四个孩子(可能是外部节点)全为黑,且黑高度相同 此时,进行局部“3+4”重构,将三个关键码的颜色改为RBR即可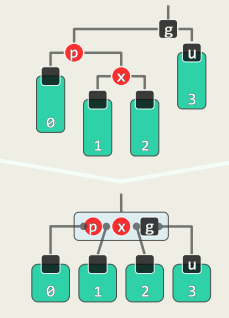
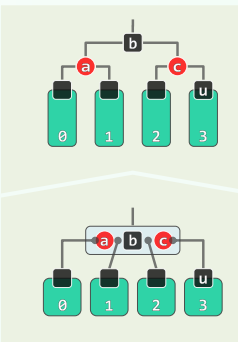
RR-2:u->color == R 在B-树中,等效于超级节点发生上溢
p与u转黑,g转红,节点分裂,关键码g上升一层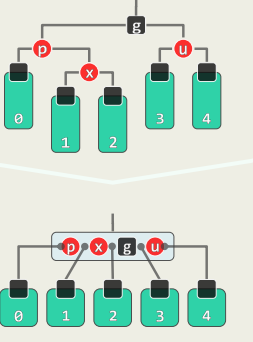
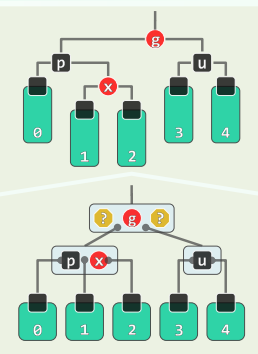
如果“双红”调整不断向上传递到树根,则强行将
g转为黑色,整棵树的黑高度加一。复杂度分析
重构、染色均只需常数时间,故只需统计其总次数
RedBlack::insert()仅需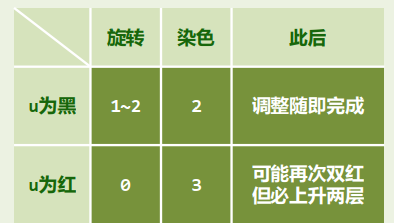
3. 删除
首先按照BST常规算法,执行
r = removeAt(x, _hot)x由孩子r接替,此时另一孩子k必为NULL。假想将另一孩子k理解为一棵黑高度与r相等的子树,且随x一并摘除。 可能违反规则3、4: 若x为红,则自然满足 若r为红,则令其与x交换颜色即可 若x与r双黑 (double black),摘除x并代之以r后,全树黑深度不再统一(相当于B-树中x所属节点发生下溢,考察r的父亲p = r->parent、兄弟s = sibling(r)
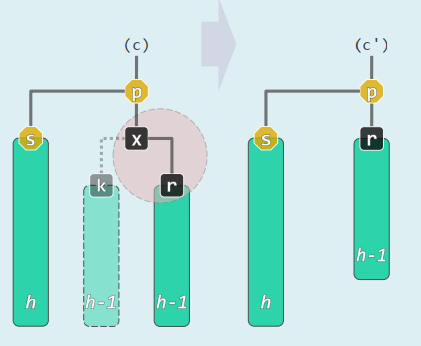
xxxxxxxxxxtemplate <typename T> bool RedBlack<T>::remove( const T & e ) { BinNodePosi<T> & x = search( e ); if ( !x ) return false; //查找定位 BinNodePosi<T> r = removeAt( x, _hot ); //删除_hot的某孩子,r指向其接替者 if ( !( --_size ) ) return true; //若删除后为空树,可直接返回 if ( !_hot ) { // 若被删除的是根,则 _root->color = RB_BLACK; //将其置黑,并 updateHeight( _root ); //更新(全树)黑高度 return true; } //至此,原x(现r)必非根 if ( BlackHeightUpdated( * _hot ) ) return true; //若父亲(及祖先)依然平衡,则无需调整 // 至此,必失衡 if ( IsRed( r ) ) { // 若替代节点r为红,则只需简单地翻转其颜色 r->color = RB_BLACK; r->height++; return true; } // 至此, r以及被其替代的x均为黑色 solveDoubleBlack( r ); //双黑调整(入口处必有 r == NULL) return true;}xxxxxxxxxxtemplate <typename T> void RedBlack<T>::solveDoubleBlack( BinNodePosi<T> r ) { BinNodePosi<T> p = r ? r->parent : _hot; if ( !p ) return; //r的父亲 BinNodePosi<T> s = (r == p->lc) ? p->rc : p->lc; //r的兄弟 if ( IsBlack( s ) ) { //兄弟s为黑 BinNodePosi<T> t = NULL; //s的红孩子(若左、右孩子皆红,左者优先;皆黑时为NULL) if ( IsRed ( s->rc ) ) t = s->rc; if ( IsRed ( s->lc ) ) t = s->lc; if ( t ) { //黑s有红孩子: BB-1 RBColor oldColor = p->color; //备份p颜色,并对t、父亲、祖父 BinNodePosi<T> b = FromParentTo( *p ) = rotateAt( t ); //旋转 if (HasLChild( *b )) { b->lc->color = RB_BLACK; updateHeight( b->lc ); } if (HasRChild( *b )) { b->rc->color = RB_BLACK; updateHeight( b->rc ); } b->color = oldColor; updateHeight( b ); //新根继承原根的颜色 } else { // 黑s无红孩子:BB-2R或BB-2B s->color = RB_RED; s->height--; //s转红 if ( IsRed( p ) ) //BB-2R:p转黑,但黑高度不变 { p->color = RB_BLACK; } else //BB-2B:p保持黑,但黑高度下降;递归修正 { p->height--; solveDoubleBlack( p ); } } } else { //BB-3 s->color = RB_BLACK; p->color = RB_RED; //s转黑, p转红 BinNodePosi<T> t = IsLChild( *s ) ? s->lc : s->rc; //取t与父s同侧 _hot = p; FromParentTo( *p ) = rotateAt( t ); //对t及其父亲、祖父做平衡调整 solveDoubleBlack( r ); //继续修正r——此时p已转红,故只能是BB-1或BB-2R }}BB-1:s为黑,且至少有一个红孩子t
“3+4”重构:
r保持黑,a,c染黑,b继承p的原色
BB-2:s为黑,且两个孩子均为黑
p为红(BB-2R)
r保持黑,s转红,p转黑。且能保证失去关键码p之后,上层节点不会继续下溢,这是因为合并之前在p之左或者右侧还应有一个黑关键码
p为黑(BB-2B)
r与p保持黑,s转红。孩子的下溢修复后,父节点继而下溢。
BB-3:s为红(其孩子均为黑)
s红转黑,p黑转红(绕p单旋)。此时r有了一个新的黑兄弟s',故而转化为前述情况。
复杂度分析
仅需
8.3 伸展树 Splay Tree
局部性 / Locality:刚被访问的数据,极有可能很快地再次被访问
伸展树:
自适应链表 self-adjusting list:节点一旦被访问,随即移到最前端 伸展树 self-adjusting binary tree:逐层伸展,使得BST的节点一旦被访问,随即调整到树根(或其附近),(实现方法:zig + zag)
Worst-Case: 倒序访问退化为链表的顺序树,
,分摊
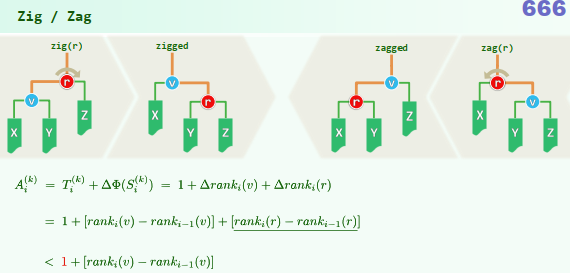
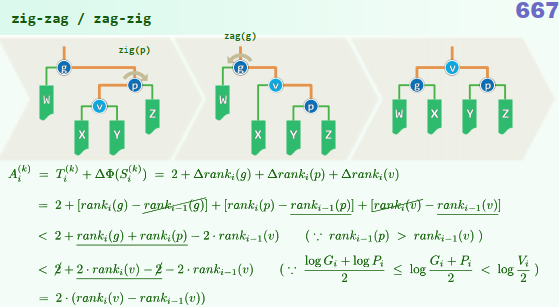
1. 双层伸展
反复考察祖孙三代,根据它们的相对位置,经两次旋转,使
上升两层,称为(子)树根 (下图中第一行为“俗”办法,第二行为“好”办法)
这种结构可以使得最坏的情况并不持续性发生(如下图所示,节点访问之后,对应路径的长度随机折半)。在这种情况下,伸展操作分摊仅需
。
要是
只有父亲,没有祖父,此时必有 ,只需要做单次旋转。但是这种情况最多在最后出现一次
2. 数学证明
定义伸展树
直觉:越平衡/倾斜的树,势能越小/大
单链:
满树:
考察对伸展树
尽管
事实上,
综合评价:
局部性强、缓存命中率极高时(即
效率甚至可以更高——自适应的
任何连续的m次查找,仅需 时间
若反复地顺序访问任一子集,分摊成本仅为常数 不能杜绝单次最坏情况,不适用于对效率敏感的场合
3. 算法实现
xxxxxxxxxxtemplate <typename T> class Splay : public BST<T> { //由BST派生protected: BinNodePosi<T> splay( BinNodePosi<T> v ); //将v伸展至根public: //伸展树的查找也会引起整树的结构调整,故search()也需重写 BinNodePosi<T> & search( const T & e ); //查找(重写) BinNodePosi<T> insert( const T & e ); //插入(重写) bool remove( const T & e ); //删除(重写)};
template <typename T> BinNodePosi<T> Splay<T>::splay( BinNodePosi<T> v ) { if ( !v ) return NULL; BinNodePosi<T> p; BinNodePosi<T> g; //父亲、祖父 while ( (p = v->parent) && (g = p->parent) ) { //自下而上,反复双层伸展 BinNodePosi<T> gg = g->parent; //每轮之后, v都将以原曾祖父为父 if ( IsLChild( * v ) ) if ( IsLChild( * p ) ) { /* zig-zig */ } else { /* zig-zag */ } else if ( IsRChild( * p ) ) { /* zag-zag */ } else { /* zag-zig */ } if ( !gg ) v->parent = NULL; //无曾祖父gg的v即树根;否则,gg此后应以v为 else ( g == gg->lc ) ? attachAsLC(v, gg) : attachAsRC(gg, v); //左或右孩子 updateHeight( g ); updateHeight( p ); updateHeight( v ); } if ( p = v->parent ) { /* 若p果真是根,只需再额外单旋一次 */ } v->parent = NULL; return v; //伸展完成, v抵达树根}伸展算法(举例:zig-zig):
查找算法
伸展树的查找, 与常规
BST::search()不同:很可能会改变树的拓扑结构,不再属于静态操作xxxxxxxxxxtemplate <typename T>BinNodePosi<T> & Splay<T>::search( const T & e ) {// 调用标准BST的内部接口定位目标节点BinNodePosi<T> p = BST<T>::search( e );// 无论成功与否,最后被访问的节点都将伸展至根_root = splay( p ? p : _hot ); //成功、失败// 总是返回根节点return _root;}插入算法
直观方法:先调用标准的
BST::search(),再将新节点伸展至根Splay::search()已集成splay(),查找失败之后, _hot即是根 既如此,何不随即就在树根附近接入新节点?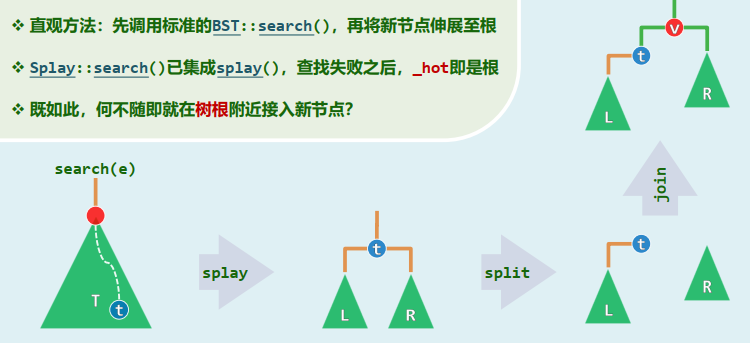
xxxxxxxxxxtemplate <typename T>BinNodePosi<T> Splay<T>::insert( const T & e ) {if ( !_root ) {_size = 1;return _root = new BinNode<T>( e );} //原树为空BinNodePosi<T> t = search( e );if ( e == t->data ) return t; //t若存在,伸展至根if ( t->data < e ) { //在右侧嫁接(rc或为空, lc == t必非空)t->parent = _root = new BinNode<T>( e, NULL, t, t->rc );if ( t->rc ) { t->rc->parent = _root; t->rc = NULL; }} else { //e < t->data,在左侧嫁接(lc或为空, rc == t必非空)t->parent = _root = new BinNode<T>( e, NULL, t->lc, t );if ( t->lc ) { t->lc->parent = _root; t->lc = NULL; }}_size++; updateHeightAbove( t ); //更新规模及t与_root的高度,插入成功return _root;} //无论如何, 返回时总有_root->data == e删除算法
直观方法:调用BST标准的删除算法,再将_hot伸展至根 注意到,
Splay::search()成功之后,目标节点即是树根 既如此,何不随即就在树根附近完成目标节点的摘除...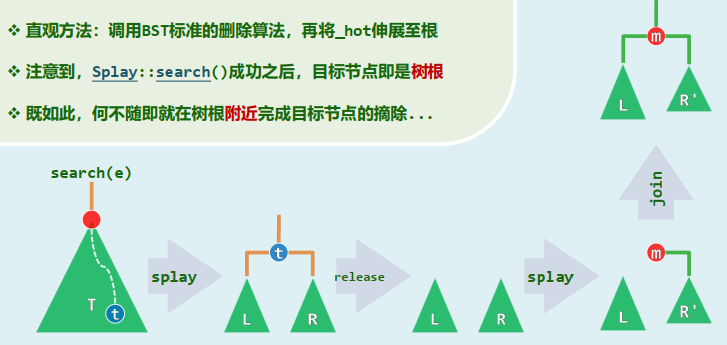
xxxxxxxxxxtemplate <typename T>bool Splay<T>::remove( const T & e ) {if ( !_root || ( e != search( e )->data ) )return false; //若目标存在,则伸展至根BinNodePosi<T> L = _root->lc, R = _root->rc;release(t); //记下左、右子树后,释放之if ( !R ) { //若R空if ( L ) L->parent = NULL; _root = L; //则L即是余树} else { //否则_root = R; R->parent = NULL;search( e ); //在R中再找e:注定失败,但最小节点必if (L) L->parent = _root; _root->lc = L; //伸展至根,故可令其以L为左子树}_size--; if ( _root ) updateHeight( _root ); //更新记录return true; //删除成功}
9 词典
9.1 散列 / Hash
循对象访问
entry = (key, value)
Map / Dictionary: 词条的集合 关键码禁止/允许雷同
get(key),put(key, value),remove(key)关键码未必可定义大小,元素类型较BST更多样 查找对象不限于最大/最小词条,接口功能较PQ更强大
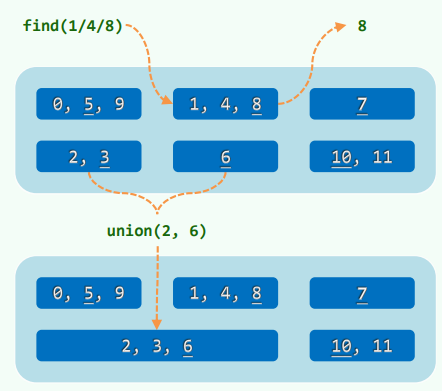
xxxxxxxxxx//Dictionarytemplate <typename K, typename V>struct Dictionary { virtual int size() = 0; virtual bool put(K, V) = 0; virtual V* get(K) = 0; virtual bool remove(K) = 0;};Notation
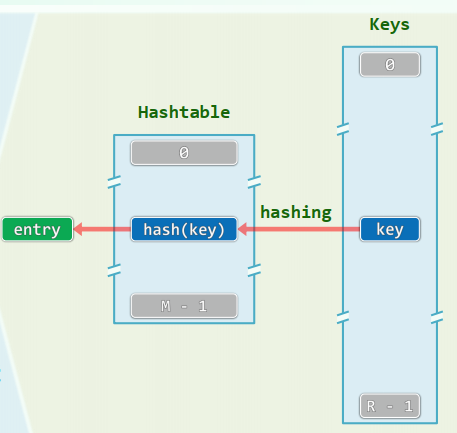
散列表/散列函数
桶(bucket):直接存放或间接指向一个词条
Bucket array ~ Hashtable 容量:
满足: 空间: 定址/杂凑/散列 根据词条的key(未必可比较)“直接”确定散列表入口(无论表有多长)
散列函数:
hash(): key |-> &entry“直接”:
1. 冲突
装填因子(load factor):
越大,空间利用率越高,冲突的情况越严重 通过降低 ,冲突程度将会有所改善,但只要数据集在动态变化,就无法彻底杜绝 完美散列(perfect hashing):实现单射的散列 采用两级散列模式 仅需
空间 关键码之间互不冲突 最坏情况下的查找时间也不过
在装填因子确定之后, 散列策略的选取将至关重要, 散列函数的设计也很有讲究
2. 设计Hash算法
- 确定 determinism:同意关键码总是被映射到同一地址
- 快速 efficiency: expected-
- 满射 surjection:尽可能充分地利用整个散列空间
- 均匀 uniform:关键码映射到散列表各位置的概率尽量接近,有效避免聚集(clustering)现象
除余法:
蝉的哲学:经长期自然选择,生命周期取素数
缺陷:
- 不动点:无论表长
- 相关性:
- 不动点:无论表长
MAD法(Multiply-Add-Divide)
数字分析(selecting digits):抽取key中的某几位,构成地址
平方取中(mid-square):去key2中间若干位,构成地址 e.g.
折叠法(folding):将key分隔成等宽的若干段,其总和作为地址 e.g.
位异或法XOR:将key分割成等宽的二进制端,经异或运算得到地址 e.g.
随机数法
多项式法:String/Object to Integer
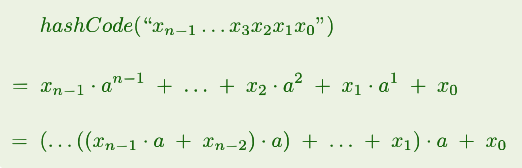

3. 处理冲突:开放散列
Open Hashing (necessarily closed addressing)
多槽位
多槽位 Multiple Slots
桶单元细分成若干槽位 存放(与同一单元)冲突的词条
只要槽位数目不太多,依然可以保证
公共溢出区
公共溢出区 Overflow Area
单独开辟一块连续空间,发生冲突的词条, 顺序存入此区域
但是一旦发生冲突,最坏情况下处理冲突词条所需的时间将正比于溢出区的规模
独立链
独立链 Linked-List Chaining / Separate Chaining
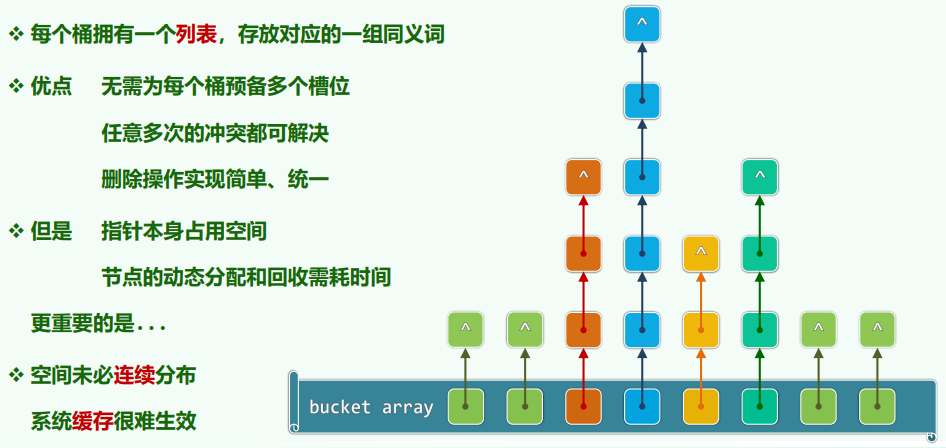
4. 处理冲突:封闭散列
Closed Hashing (necessarily open addressing): 只要有必要,任何散列桶都可以接纳任何词条
开放定址
开放定址
Probe Sequence / Chain 为每个词条,都需事先约定多干备用桶,优先级逐次下降
查找算法(线性试探)
沿试探链,逐个转向紧邻的桶,直到命中(成功);或者抵达一个空桶(存在则必能找到?) 而失败
在散列表内部解决冲突,无需附加的指针、链表或溢出区等,整体结构保持简洁 但是,新增非同义词之间的冲突;数据堆积(clustering)现象严重 通过装填因子,冲突与堆积都可有效控制——缓存生效,所以可以很快
问题:插入 + 删除
插入:新词条若尚不存在,则存入试探终止处的空桶 试探链:可能因而彼此串接、 重叠(未必是synonym)
删除:简单地清楚命中的桶? 经过它的试探链都将因此断裂,导致后续词条丢失——明明存在,却访问不到

懒惰删除
懒惰删除
xxxxxxxxxxBitmap* removed; //用Bitmap懒惰地标记被删除的桶int L; //被标记桶的数目查找词条时,被视作“必不匹配的非空桶”,试探链在此得以延续 插入词条时,被视作“必然匹配的空闲桶”,可以用来存放新词条
xxxxxxxxxxtemplate <typename K, typename V>int Hashtable<K, V>::probe4Hit(const K& k) {int r = hashCode(k) % M; //按除余法确定试探链起点while ( ( ht[r] && (k != ht[r]->key) ) || removed->test(r) )r = ( r + 1 ) % M; //线性试探(跳过带懒惰删除标记的桶)return r; //调用者根据ht[r]是否为空及其内容,即可判断查找是否成功}template <typename K, typename V>int Hashtable<K, V>::probe4Free(const K& k) {int r = hashCode(k) % M; //按除余法确定试探链起点while ( ht[r] )r = (r + 1) % M; //线性试探,直到空桶(无论是否带有懒惰删除标记)return r; //只要有空桶,线性试探迟早能找到}
重散列
重散列 Rehashing
xxxxxxxxxxtemplate <typename K, typename V> //随着装填因子增大,冲突概率、排解难度都将激增void Hashtable<K, V>::rehash() { //此时,不如“集体搬迁”至一个更大的散列表int oldM = M;Entry<K, V>** oldHt = ht;ht = new Entry<K, V>*[ M = primeNLT( 4 * N ) ];N = 0; //新表“扩”容memset( ht, 0, sizeof( Entry<K, V>* ) * M ); //初始化各桶release( removed );removed = new Bitmap(M);L = 0; //懒惰删除标记for ( int i = 0; i < oldM; i++ ) //扫描原表if ( oldHt[i] ) //将每个非空桶中的词条put( oldHt[i]->key, oldHt[i]->value ); //转入新表release( oldHt ); //释放——因所有词条均已转移,故只需释放桶数组本身}懒惰删除的算法使得装填因子的真实值被低估,因而“扩”容采用
插入:
xxxxxxxxxxtemplate <typename K, typename V>bool Hashtable<K, V>::put( K k, V v ) {if ( ht[ probe4Hit( k ) ] )return false; //雷同元素不必重复插入int r = probe4Free( k ); //为新词条找个空桶(只要装填因子控制得当,必然成功)ht[ r ] = new Entry<K, V>( k, v );++N; //插入if ( removed->test( r ) ) {removed->clear( r );--L;} //懒惰删除标记if ( (N + L) * 2 > M )rehash(); //若装填因子高于50%,重散列return true;}删除:
xxxxxxxxxxtemplate <typename K, typename V>bool Hashtable<K, V>::remove( K k ) {int r = probe4Hit( k );if ( !ht[r] )return false; //确认目标词条确实存在release( ht[r] );ht[r] = NULL;--N; //清除目标词条removed->set(r);++L; //更新标记、计数器if ( 3 * N < L )rehash(); //若懒惰删除标记过多, 重散列return true;}
平方试探
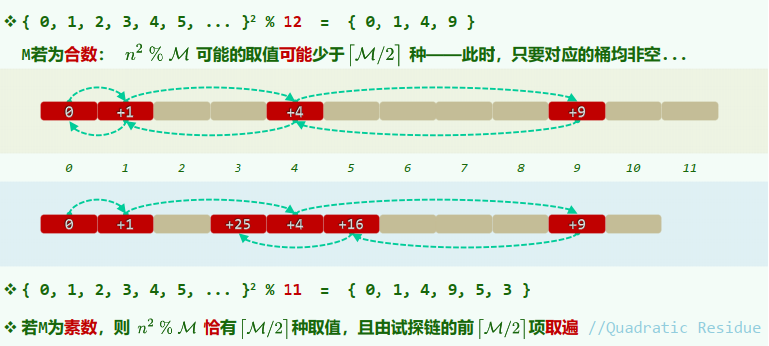
平方试探 Quadratic Probing
Definition: 以平方数为距离,确定下一试探桶单元
数据聚集现象有所缓解 试探链上,各桶间距线性递增 一旦冲突,可“聪明”地跳离是非之地 对于大散列表,I/O操作有所增加
xxxxxxxxxx[hash(key) + 1] % M[hash(key) + 4] % M[hash(key) + 9] % M[hash(key) + 16] % M

素数表长时,只要
双向平方试探
双向平方试探
Definition: 交替地沿两个方向试探,均按平方确定距离
xxxxxxxxxx[hash(key) + 1] % M[hash(key) + 4] % M[hash(key) + 9] % M[hash(key) + 16] % M[hash(key) - 1] % M[hash(key) - 4] % M[hash(key) - 9] % M[hash(key) - 16] % M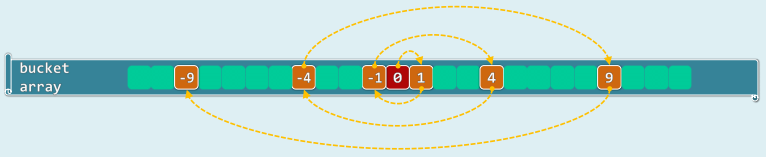
两类素数:

双散列 Double Hashing
预先约定第二散列函数:
冲突时,由其偏移增量,确定下一试探位置:
- 线性试探:
- 平方试探:
9.2 桶排序
1. 基本算法实现
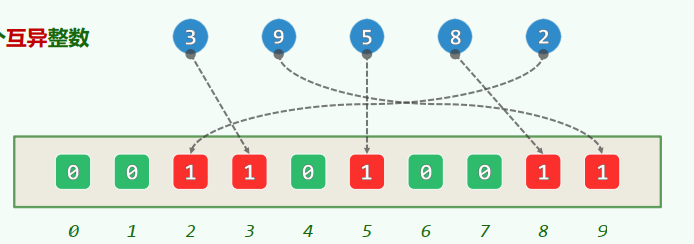
- 对
空间:
时间: 初始化:for i = 0 to m - 1, let
= 0 映射:for each key in the input, let = 1 枚举:for i = 0 to m - 1, output i if = 1
- 允许重复(可能
空间:
时间:
2. 最大缝隙 MaxGap
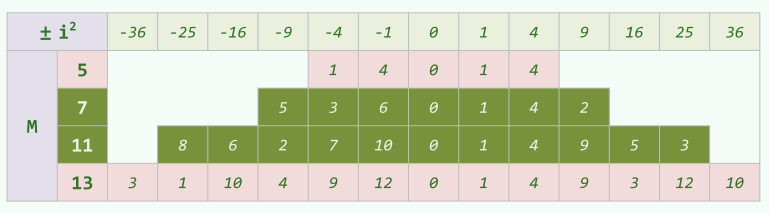
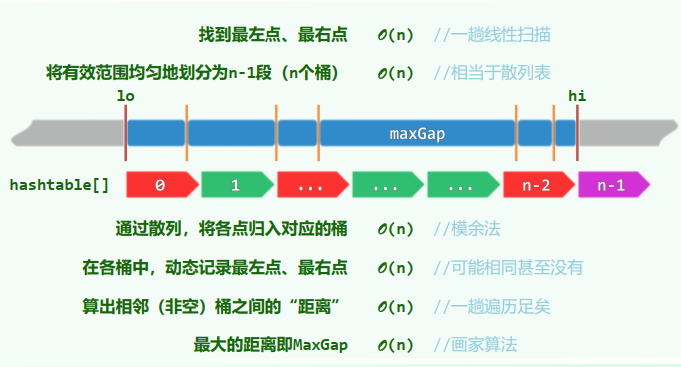
任意
个互异点均将实轴氛围 段有界区间,其中的哪一段最长?
线性算法:
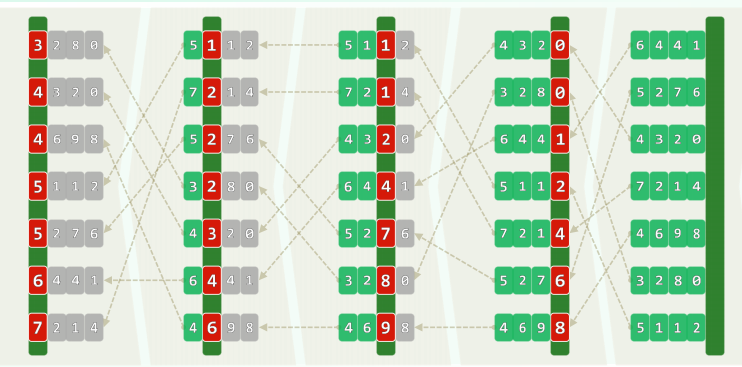
9.3 基数排序 Radixsort
有时,关键码由多个域组成: kd , kt-1 , ... , k1 // (suit, point) in bridge 若将各域视作字母,则关键码即单词——按词典的方式排序(lexicographic order)
- 自k1到kt(低位优先),依次以各域为序做一趟桶排序

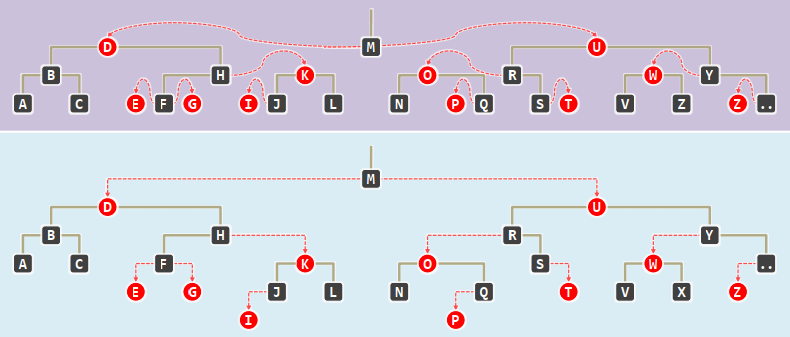
9.4 跳转表 Skip List
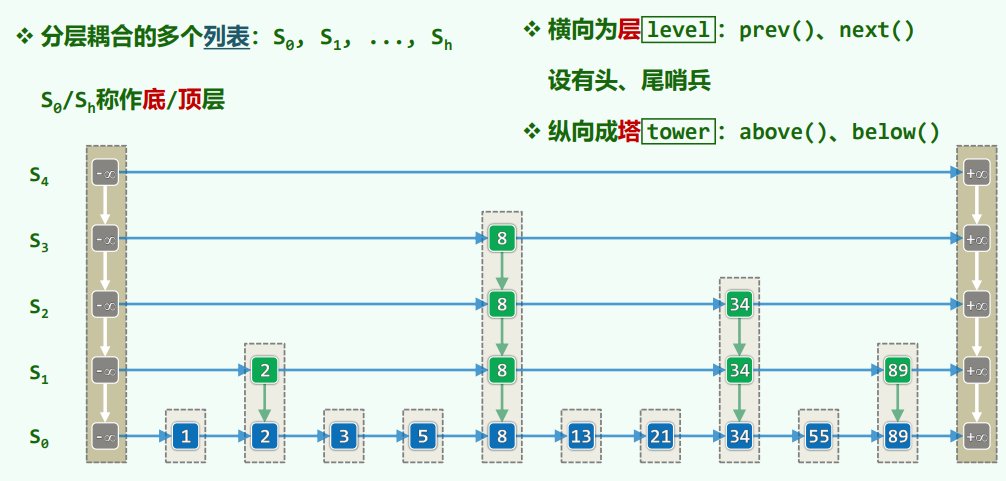
xxxxxxxxxxtemplate <typename T> using QNodePosi = QNode<T>*; //节点位置template <typename T> struct QNode { //四联节点 T entry; //所存词条 QNodePosi<T> pred, succ, above, below; //前驱、后继、上邻、下邻 QNode( T e = T(), QNodePosi<T> p = NULL, QNodePosi<T> s = NULL, QNodePosi<T> a = NULL, QNodePosi<T> b = NULL ) //构造器 : entry(e), pred(p), succ(s), above(a), below(b) {} QNodePosi<T> insert( T const& e, QNodePosi<T> b = NULL ); //将e作为当前节点的后继、b的上邻插入};
template <typename T> struct Quadlist { //四联表 int _size; //节点总数 QNodePosi<T> header, trailer; //头、尾哨兵 void init(); int clear(); //初始化、清除 Quadlist() { init(); } //构造 ~Quadlist() { clear(); delete header; delete trailer; } //析构 T remove( QNodePosi<T> p ); //删除p QNodePosi<T> insert(T const & e, QNodePosi<T> p, QNodePosi<T> b = NULL); //将e作为p的后继、b的上邻插入};
template < typename K, typename V > struct Skiplist :public Dictionary<K, V>, public List< Quadlist< Entry<K, V> >* > { Skiplist() //即便为空,也有一层空列表 { insertAsFirst( new Quadlist< Entry<K, V> > ); }; QNodePosi< Entry<K, V> > search( K ); //由关键码查询词条 int size() {return empty() ? 0 : last()->data->size();} //词条总数 int height() { return List::size(); } //层高,即Quadlist总数 bool put( K, V ); //插入(Skiplist允许词条重复,故必然成功) V * get( K ); //读取 bool remove( K ); //删除};
空间性能
逐层随机减半:
1. 查找
时间复杂度:
xxxxxxxxxxtemplate <typename K, typename V> //关键码不大于k的最后一个词条(所对应塔的基座)QNodePosi< Entry<K, V> > Skiplist<K, V>::search( K k ) {for ( QNodePosi< Entry<K, V> > p = first()->data->header; ; ) //从顶层的首节点出发if ( (p->succ->succ) && (p->succ->entry.key <= k) )p = p->succ; //尽可能右移else if ( p->below ) p = p->below; //水平越界时,下移else return p; //验证:此时p符合输出约定(可能是最底层列表的header)} //体会:得益于哨兵的设置,哪些环节被简化了?
时间性能
查找时间取决于横向、纵向的累计跳转次数
整张表的期望高度为

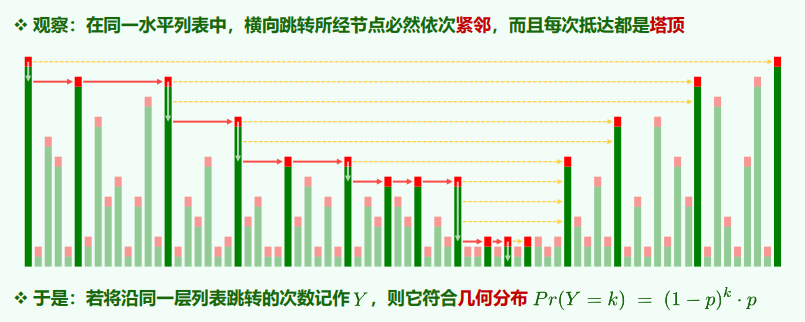

2. 插入与删除
时间复杂度:
xxxxxxxxxxtemplate <typename K, typename V>bool Skiplist<K, V>::put(K k, V v) {Entry<K, V> e = Entry<K, V>( k, v ); //待插入的词条QNodePosi< Entry<K, V> > p = search( k ); //查找插入位置:新塔将紧邻其右,逐层生长ListNodePosi< Quadlist<Entry<K, V>>* > qlist = last(); //首先在最底层QNodePosi<Entry<K, V>> b = qlist->data->insert(e, p); //创建新塔的基座while ( rand() & 1 ) {// 建塔while ( p->pred && !p->above ) p = p->pred; //找出不低于此高度的最近前驱if ( !p->pred && !p->above ) { //若该前驱是header,且已是最顶层,则insertAsFirst( new Quadlist< Entry<K, V> > ); //需要创建新的一层first()->data->header->below = qlist->data->header;qlist->data->header->above = first()->data->header;}p = p->above; qlist = qlist->pred; //上升一层,并在该层b = qlist->data->insert( e, p, b ); //将新节点插入p之后、b之上}return true; //Dictionary允许重复元素,故插入必成功} //体会:得益于哨兵的设置,哪些环节被简化了?
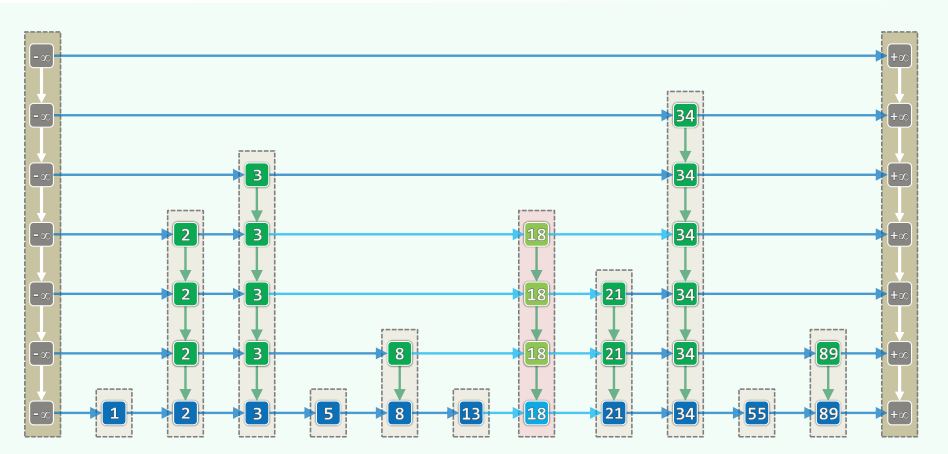
xxxxxxxxxxtemplate <typename K, typename V>bool Skiplist<K, V>::remove( K k ) {QNodePosi< Entry<K, V> > p = search( k ); //查找目标词条if ( !p->pred || (k != p->entry.key) ) return false; //若不存在,直接返回/* ... 1. 预备 ... */ListNodePosi< Quadlist<Entry<K, V>>* > qlist = last(); //从底层Quadlist开始while ( p->above ) { qlist = qlist->pred; p = p->above; } //升至塔顶/* ... 2. 拆塔 ... */do {QNodePosi<Entry<K, V>> lower = p->below; //记住下一层节点qlist->data->remove(p); //删除当前层节点,再p = lower; qlist = qlist->succ; //转入下一层} while (qlist->succ); //直到塔基/* ... 3. 删除空表 ... */while ( (1 < height()) && (first()->data->_size < 1) ) { //逐层清除List::remove(first());first()->data->header->above = NULL;} //已不含词条的Quadlist(至少保留最底层空表)return true; //删除成功} //体会:得益于哨兵的设置,哪些环节被简化了?
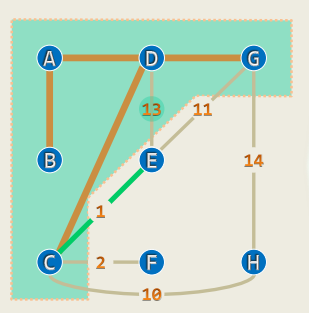
10 图 Graph
10.1 基本概念
节点数
同一条边的两个顶点——彼此邻接(adjacency) 同一顶点自我邻接——构成自环(self-loop) 不含自环及重边——即为简单图(simple graph) 非简单图(non-simple)暂不讨论
顶点与其所属的边——彼此关联(incidence) 度(degree/valency)——与同一顶点关联的边数
若邻接顶点u和v的次序无所谓,则(u, v)为无向边(undirected edge) 所有边均无方向的图,即无向图(undigraph) 反之,有向图(digraph)中均为有向边(directed edge)。u,v分别称作边(u, v)的尾(tail)和头(head) 无向边、有向边并存的图,称作混合图(mixed graph)
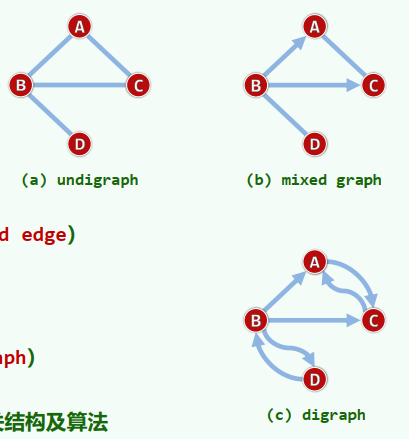
路径
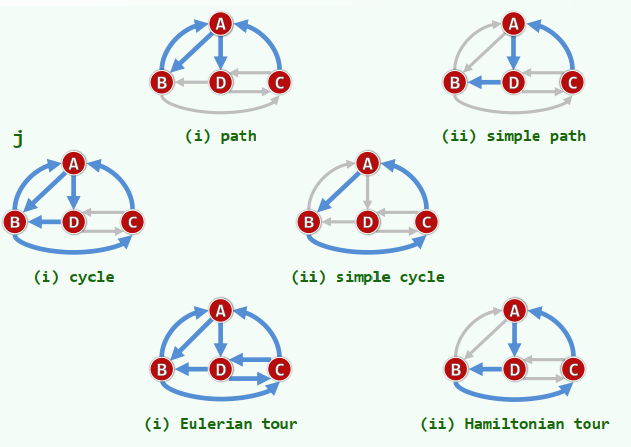
图
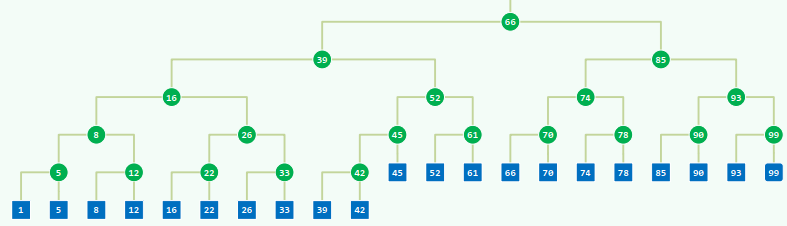
xxxxxxxxxxtemplate <typename Tv, typename Te> class Graph {private: void reset() { //所有顶点、边的辅助信息复位 for ( Rank v = 0; v < n; v++ ) { //顶点 status(v) = UNDISCOVERED; dTime(v) = fTime(v) = -1; parent(v) = -1; priority(v) = INT_MAX; for ( Rank u = 0; u < n; u++ ) //边 if ( exists(v, u) ) type(v, u) = UNDETERMINED; } //for } //resetpublic: int n, e; //顶点、边数目 /* ... 顶点操作、边操作、图算法: 无论如何实现,接口必须统一 ... */} //Graph1. 邻接矩阵 adjacency matrix
记录顶点之间的邻接关系——对应:矩阵元素(图中可能存在的边)
既然只考察简单图,对角线统一设置为0 空间复杂度为
,与图中实际的边数无关
xxxxxxxxxxusing VStatus = enum { UNDISCOVERED, DISCOVERED, VISITED };template <typename Tv> struct Vertex { //不再严格封装 Tv data; int inDegree, outDegree; VStatus status; //(如上三种)状态 int dTime, fTime; //时间标签 Rank parent; //在遍历树中的父节点 int priority; //在遍历树中的优先级(最短通路、极短跨边等) Vertex( Tv const & d ) : data( d ), inDegree( 0 ), outDegree( 0 ), status( UNDISCOVERED ), dTime( -1 ), fTime( -1 ), parent( -1 ), priority( INT_MAX ) {}};
using EType = enum { UNDETERMINED, TREE, CROSS, FORWARD, BACKWARD };template <typename Te> struct Edge { //不再严格封装 Te data; //数据 int weight; //权重 EType type; //在遍历树中所属的类型 Edge( Te const & d, int w ) : data(d), weight(w), type(UNDETERMINED) {}};xxxxxxxxxxtemplate <typename Tv, typename Te> class GraphMatrix : public Graph<Tv, Te> {private: Vector< Vertex<Tv> > V; //顶点集 Vector< Vector< Edge<Te>* > > E; //边集public: // 操作接口: 顶点相关、 边相关、 ... GraphMatrix() { n = e = 0; } //构造 ~GraphMatrix() { //析构 for ( Rank v = 0; v < n; v++ ) for ( Rank u = 0; u < n; u++ ) delete E[v][u]; //清除所有边记录 }};
静态操作
顶点的读写
xxxxxxxxxxTv & vertex(Rank v) { return V[v].data; } //数据int inDegree(Rank v) { return V[v].inDegree; } //入度int outDegree(Rank v) { return V[v].outDegree; } //出度VStatus & status(Rank v) { return V[v].status; } //状态int & dTime(Rank v) { return V[v].dTime; } //时间标签dTimeint & fTime(Rank v) { return V[v].fTime; } //时间标签fTimeRank & parent(Rank v) { return V[v].parent; } //在遍历树中的父亲int & priority(Rank v) { return V[v].priority; } //优先级数边的读写
xxxxxxxxxxbool exists( Rank v, Rank u ) { //判断边(v, u)是否存在(短路求值)return (v < n) && (u < n) && E[v][u] != NULL;} //以下假定exists(v, u) = trueTe & edge( Rank v, Rank u ) { return E[v][u]->data; } //数值EType & type( Rank v, Rank u ) { return E[v][u]->type; } //类型int & weight( Rank v, Rank u ) { return E[v][u]->weight; } //权重邻点的枚举
xxxxxxxxxxRank firstNbr( Rank v ) { return nextNbr( v, n ); } //假想哨兵Rank nextNbr( Rank v, Rank u ) { //若已枚举至邻居u, 则转向下一邻居while ( -1 < u ) && !exists( v, --u ) ); //逆向顺序查找return u;} //O(n)——改用邻接表,可提高至O(1 + outDegree(v))
动态操作
边的插入
xxxxxxxxxxvoid insert( Te const & edge, int w, Rank v, Rank u ) {if ( exists(v, u) ) return; //忽略已有的边E[v][u] = new Edge<Te>( edge, w ); //创建新边(权重为w)e++; //更新边计数V[v].outDegree++; //更新顶点v的出度V[u].inDegree++; //更新顶点u的入度}边的删除
xxxxxxxxxxTe remove( Rank v, Rank u ) { //删除(已确认存在的) 边(v, u)Te eBak = edge(v, u); //备份边(v, u)的信息delete E[v][u]; E[v][u] = NULL; //删除边(v, u)e--; //更新边计数V[v].outDegree--; //更新顶点v的出度V[u].inDegree--; //更新顶点u的入度return eBak; //返回被删除边的信息}顶点插入
xxxxxxxxxxRank insert( Tv const & vertex ) { //插入顶点,返回编号for ( Rank u = 0; u < n; u++ ) E[u].insert( NULL ); n++; //①E.insert( Vector< Edge<Te>* >( n, n, NULL ) ); //②③return V.insert( Vertex<Tv>( vertex ) ); //④}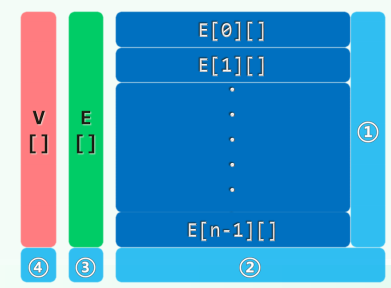
顶点删除
xxxxxxxxxxTv remove( Rank v ) { //删除顶点及其关联边,返回该顶点信息for ( Rank u = 0; u < n; u++ ) //删除所有出边if ( exists( v, u ) ) {delete E[v][u]; V[u].inDegree--; e--;}E.remove(v); n--; //删除第v行Tv vBak = vertex( v ); V.remove( v ); //备份之后,删除顶点vfor ( Rank u = 0; u < n; u++ ) //删除所有入边及第v列if ( Edge<Te> * x = E[u].remove( v ) ){ delete x; V[u].outDegree--; e--; }return vBak; //返回被删除顶点的信息}
性能分析
- 直观,易于理解和实现
- 适用范围广泛,尤其适用于稠密图(dense graph)
- 判断两点之间是否存在联边:
- 扩展性(scalability):得益于Vector良好的控制策略,空间溢出等情况可被“透明的”处理
- 但是!
- 平面图(planar graph):可嵌入于平面的图,满足
- 稀疏图(sparse graph):空间利用率同样很低,可采用压缩存储技术
2. 关联矩阵 incidence matrix
记录顶点与边之间的关联关系——对应:矩阵元素(每条边的两个节点)
空间复杂度为
空间利用率 解决某些问题时十分有效

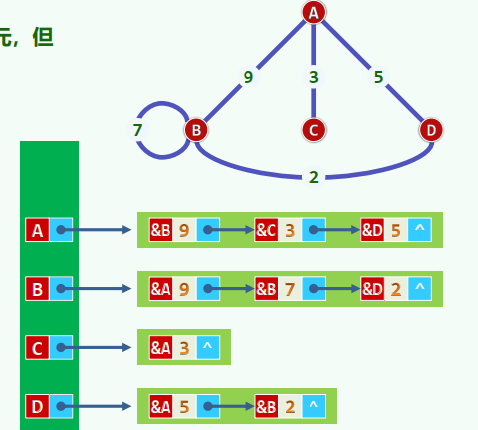
3. 邻接表
空间复杂度
- 有向图:
- 无向图:
- 适用于稀疏图
- 平面图 =
时间复杂度
- 建立邻接表(递增式构造):
- 枚举所有以顶点v为尾的弧:
- 枚举(无向图中)顶点v的邻居:
- 枚举所有以顶点v为头的弧:
- 计算顶点v的出度/入度:
增加度数记录域:
- 给定顶点u和v,判断是否
10.2 广度优先搜索 BFS
Breadth-First Search
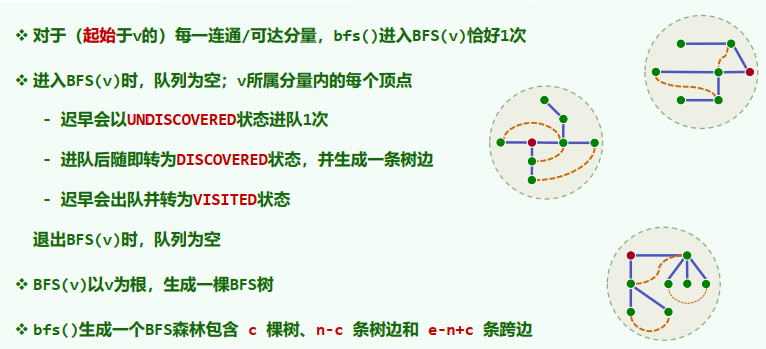
相当于树的层次遍历 事实上,BFS也的确会构造出原图的一棵支撑树(BFS tree)
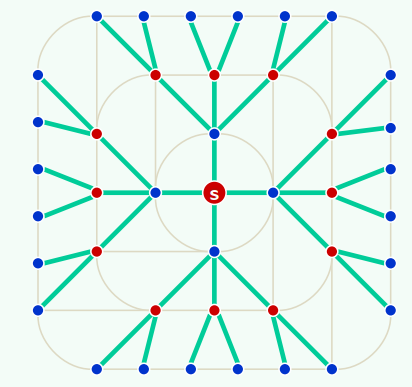
xxxxxxxxxxtemplate <typename Tv, typename Te>void Graph<Tv, Te>::BFS( Rank v, int & clock ) { Queue<Rank> Q; status(v) = DISCOVERED; Q.enqueue(v); //初始化 while ( ! Q.empty() ) { //反复地 Rank v = Q.dequeue(); dTime(v) = ++clock; //取出队首顶点v,并 for ( Rank u = firstNbr(v); -1 < u; u = nextNbr(v, u) ) if ( UNDISCOVERED == status(u) ) { //若u尚未被发现,则 status(u) = DISCOVERED; Q.enqueue(u); //发现该顶点 type(v, u) = TREE; parent(u) = v; //引入树边 } else //若u已被发现(正在队列中),或者甚至已访问完毕(已出队列),则 type(v, u) = CROSS; //将(v, u)归类于跨边 status(v) = VISITED; //至此,当前顶点访问完毕 }}1. 连通分量 + 可达分量
问题:给定无向图,找出其中任一顶点s所在的连通图 给定有向图,找出源自其中任一顶点s的可达分量
算法:从s出发做BFS,输出所有被发现的顶点,队列为空后立即终止
xxxxxxxxxxtemplate <typename Tv, typename Te>void Graph<Tv, Te>::bfs( Rank s ) { //s为起始顶点 reset(); int clock = 0; Rank v = s; //初始化O(n+e) do //逐一检查所有顶点,一旦遇到尚未发现的顶点 if ( UNDISCOVERED == status(v) ) //累计O(n) BFS( v, clock ); //即从该顶点出发启动一次BFS while ( s != (v = ((v + 1) % n)) ); //按序号访问,不漏不重} //无论共有多少连通/可达分量,bfs均可遍历它们,而且自身累计仅需线性时间2. 边分类


3. BFS树 / 森林
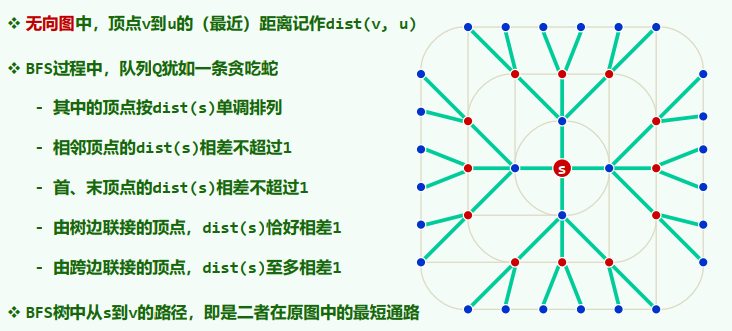
4. 最短路径
无向图中,顶点v到u的举例记作
5. Erdös Number: collaborative distance

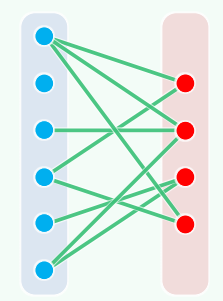
6. Bipartite Graph (Bigraph)
7. Eccentricity / Radius / Diameter / Center
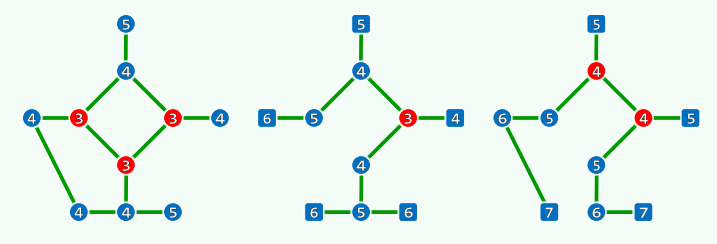
8. Knights of the Round Table
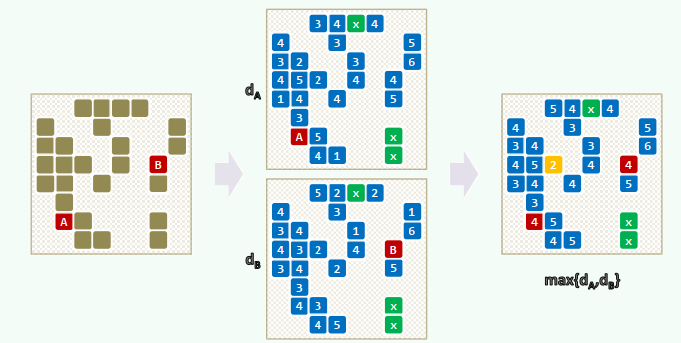
10.3 深度优先搜索 DFS
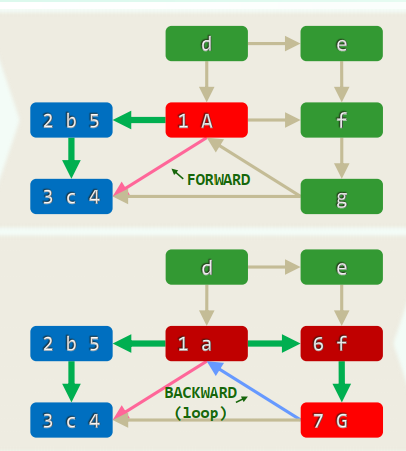
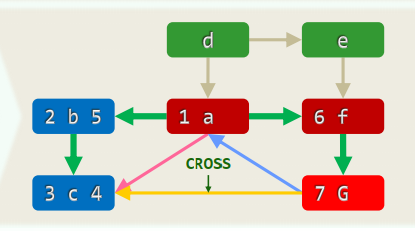
Depth-First Search
相当于树的先序遍历 事实上,DFS也的确会构造出原图的一棵支撑树(DFS tree)
xxxxxxxxxxtemplate <typename Tv, typename Te>void Graph<Tv, Te>::DFS( Rank v, int & clock ) { dTime(v) = ++clock; status(v) = DISCOVERED; //发现当前顶点v for ( Rank u = firstNbr(v); -1 < u; u = nextNbr(v, u) ) //v的邻居u switch ( status(u) ) { case UNDISCOVERED: //u尚未发现,意味着支撑树可在此拓展 type(v, u) = TREE; parent(u) = v; DFS( u, clock ); break; //递归 case DISCOVERED: //u已被发现但尚未访问完毕,应属被后代指向的祖先 type(v, u) = BACKWARD; break; default: //u已访问完毕(VISITED有向图),则视承袭关系分前向边或跨边 type(v, u) = dTime(v) < dTime(u) ? FORWARD : CROSS; break; } status(v) = VISITED; fTime(v) = ++clock; //至此,当前顶点v方告访问完毕}1. 连通分量 + 可达分量
xxxxxxxxxxtemplate <typename Tv, typename Te>void Graph<Tv, Te>::dfs( Rank s ) { //s为起始顶点 reset(); int clock = 0; Rank v = s; //初始化 do //逐一检查所有顶点,一旦遇到尚未发现的顶点v if ( UNDISCOVERED == status(v) ) DFS( v, clock ); //即从v出发启动一次DFS while ( s != (v = ((v + 1) % n)) ); //按序号访问,不漏不重}2. DFS树 / 森林
从顶点s出发的DFS 在无向图中将访问与s连通的所有顶点(connectivity) 在有向图中将访问由s可达的所有顶点(reachability)
所有DFS树构成DFS森林
活跃期:status[], dtime[]和ftime[]即可对各边分类...
边分类:
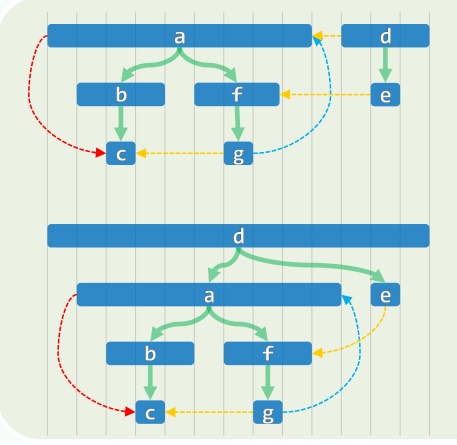
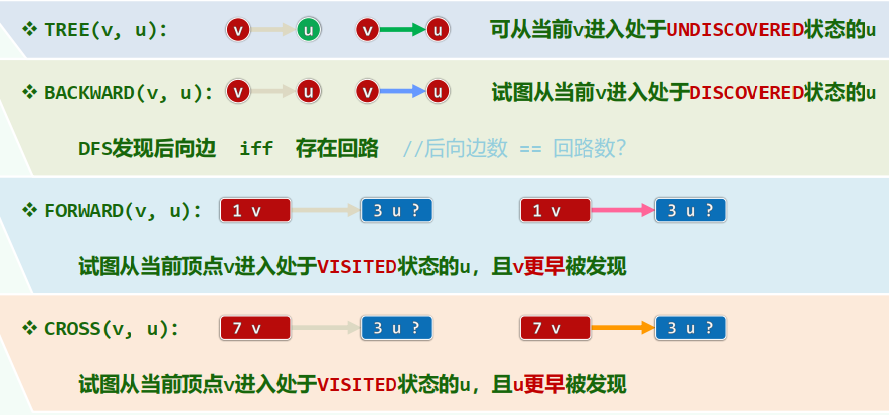
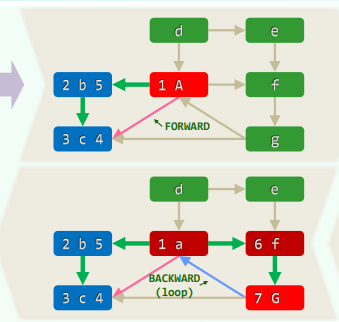
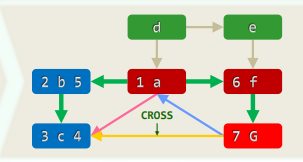
3. 遍历算法应用举例
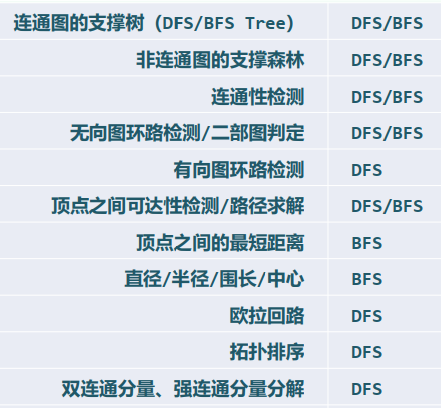
拓扑排序
有向无环图:Directed Acyclic Graph
任给有向图G(不一定是DAG),尝试将所有顶点排成一个线性序列,使其次序与原图相容(每一顶点都不会通过边指向前驱顶点)
若原图存在回路(即并非DAG),检查并报告。否则,给出一个相容的线性序列
策略:顺序输出零入度顶点
xxxxxxxxxx//将所有入度为零的顶点存入栈S,取空队列Q:O(n)while ( ! S.empty() ) { //O(n) Q.enqueue( v = S.pop() ); //栈顶v转入队列 for each edge( v, u ) //v的邻接顶点u若入度仅为1 if ( u.inDegree < 2 ) S.push( u ); //则入栈 G = G \ { v }; //删除v及其关联边(邻接顶点入度减1)} //总体O(n + e)return |G| ? "NOT_A_DAG" : Q; //残留的G空,当且仅当原图可拓扑排序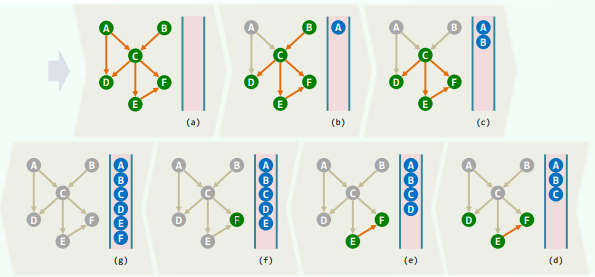
零出度算法:逆序输出零出度顶点
(基于DFS,借助栈S) 对图G做DFS,其间 每当有顶点被标记为VISITED,则将其压入S 一旦发现有后向边,则报告“NOT_A_DAG”并退出 DFS结束后,顺序弹出S中的各个顶点 各节点按ftime逆序排列,即是拓扑排序 复杂度与DFS相当,也是
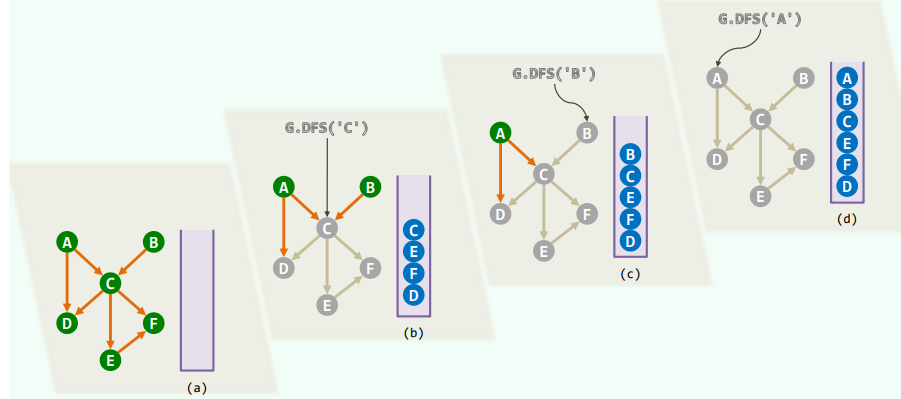
xxxxxxxxxxtemplate <typename Tv, typename Te> //顶点类型、边类型bool Graph<Tv, Te>::TSort( Rank v, int & clock, Stack<Tv>* S ) { dTime(v) = ++clock; status(v) = DISCOVERED; //发现顶点v for ( Rank u = firstNbr(v); u < INT_MAX; u = nextNbr(v, u) ) //考查v的每一邻居u switch ( status(u) ) { //并视u的状态分别处理 case UNDISCOVERED: parent(u) = v; type(v, u) = TREE; if ( ! TSort(u, clock, S) ) //从顶点u处深入 return false; break; case DISCOVERED: //一旦发现后向边(非DAG) type(v, u) = BACKWARD; //则退出而不再深入 return false; default: //VISITED (digraphs only) type(v, u) = dTime(v) < dTime(u) ? FORWARD : CROSS; break; } status(v) = VISITED; S->push( vertex(v) ); //顶点被标记为VISITED时入栈 return true;}
10.4 优先级搜索 PFS
不同顶点选取策略,取决于存放和提供顶点的数据结构——Bag
此类结构,为每个顶点v维护一个优先级数——priority(v)
每个顶点都有初始优先级数,并可能随算法的推进而调整
通常的习惯是,优先级数越大/小,优先级越低/高
xxxxxxxxxxtemplate <typename Tv, typename Te>template <typename PU> //优先级更新器(函数对象)void Graph<Tv, Te>::PFS( Rank v, PU prioUpdater ) { //PU的策略 priority(v) = 0; status(v) = VISITED; parent(v) = -1; //起点v加至PFS树中 while (1) { //将下一顶点和边加至PFS树中 // update for ( Rank u = firstNbr(v); -1 < u; u = nextNbr(v, u) ) //对v的每一个邻居u prioUpdater( this, v, u ); //更新其优先级及其父亲 // select for ( int shortest = INT_MAX, u = 0; u < n; u++ ) if ( UNDISCOVERED == status(u) ) //从尚未加入遍历树的顶点中 if ( shortest > priority(u) ) //选出下一个 { shortest = priority(u); v = u; } //优先级最高的顶点v // visit if ( VISITED == status(v) ) break; //直至所有顶点均已加入 status(v) = VISITED; type( parent(v), v ) = TREE; //将v加入树 } //while} //如何推广至非连通图?复杂度:
- 更新树外顶点的优先级:
- 选出新的优先级最高者:

10.5 Dijkstra算法:最短路径
Dijkstra:SSSP / Single-Source Shortest Path 给定顶点s,计算s到其余各个顶点的最短路径及长度 Floyd-Warshall:APSP / All-Pairs Shortest Path 找出每对顶点u和v之间的最短路径及长度
1. 最短路径树
Lemma:任一最短路径的前缀,也是一条最短路径
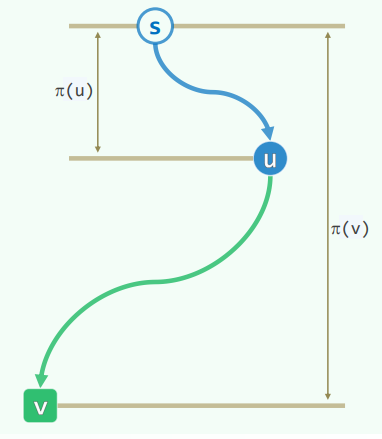
消除歧义:
各边权重均为正,否则 有可能出现总权重非正的环路 以致最短路径无从定义 有负权重的边时,即便多有环路总权重皆为正,Dijkstra算法依然可能失效 任意两点之间,最短路径唯一 在不影响计算结果的前提下,总可通过适当扰动予以保证(*)
Shortest Path Tree:
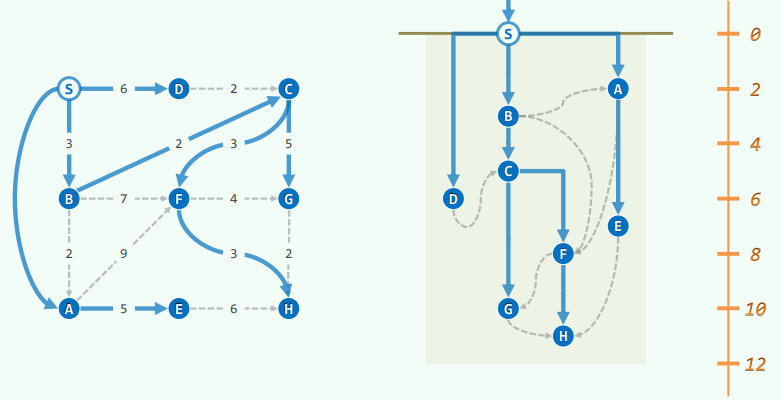
2. 算法实现
, let 于是套用PFS框架,为将 扩充至 ,只需 选出优先级最高的跨边 及其对应顶点 ,并将其加入 随后,更新 中所有顶点的优先级(数) 注意:优先级数随后可能改变(降低)的顶点,必与 邻接 因此,只需枚举 的每一邻接顶点 ,并取 以上完全符合PFS的框架,唯一要做的工作无非是按照 prioUpdater()规范,编写一个优先级(数)更新器...
xxxxxxxxxx//Prority Updater ~ DijkPUg->pfs( 0, DijkPU<char, Rank>() ); //从顶点0出发,启动Dijkstra算法template <typename Tv, typename Te> struct DijkPU { virtual void operator()( Graph<Tv, Te>* g, Rank v, Rank u ) { //对v的每个 if ( UNDISCOVERED != g->status(u) ) return; //尚未被发现的邻居u,按 if ( g->priority(u) > g->priority(v) + g->weight(v, u) ) { //Dijkstra g->priority(u) = g->priority(v) + g->weight(v, u); //策略 g->parent(u) = v; //做松弛 } }};
10.6 Floyd-Warshall算法:最短路径
给定带权网络G,计算其中所有点对之间的最短距离 应用:确定G的中心点(center) radius(G, s) = s的半径 = 所有顶点到s的最大距离 中心点 = 半径最小的顶点s 直觉:依次将个顶点作为源点,调用Dijkstra算法 时间 =
思路:图矩阵 ~ 最短路径矩阵 效率: ,与执行n次Dijkstra相同 优点:形式简单、算法紧凑、便于实现;允许负权边(但不允许负权环路)
1. 思路
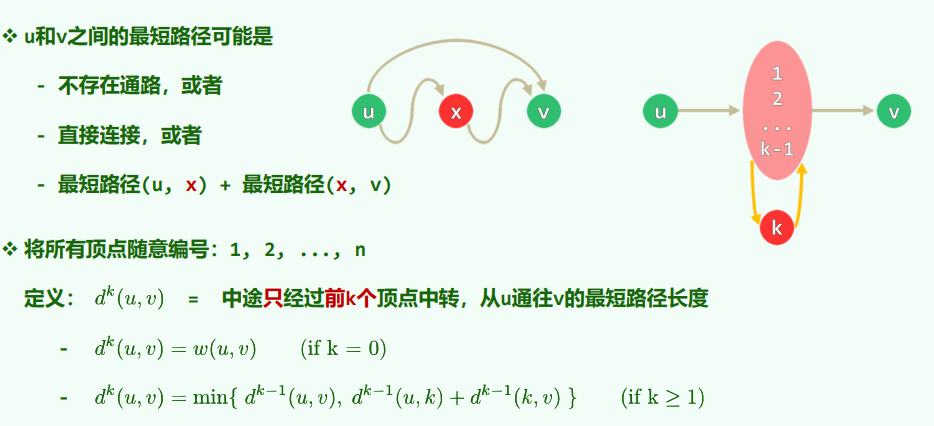
动态规划:
xxxxxxxxxxfor k in range(0, n) for u in range(0, n) for v in range(0, n) A[u][v] = min(A[u][v], A[u][k] + A[k][v])
10.7 Prim算法:最小支撑树 MST
连通网络
的子图 支撑 / spanning = 覆盖N中所有顶点 树 / tree = 连通且无环, 同一网络的支撑树,未必唯一 minimum = optimal: 达到最小
1. Prim算法:极短跨边
任何环路C上的最长边f,都不会被MST采用 否则,移除f之后,MST将分裂为两棵树,将其视作一个割,则C上必有该割的另一跨边e,既然
,那么只要用 替换f,就可以的到一棵总权重更小的支撑树 若uv是某一割的一条极短跨边,则必存在一棵包含uv的MST 任一MST都必然通过极短跨边连接每一割
递增式构造:
,其中
注意:当MST不唯一时,由极短跨边构成的支撑树,未必就是一棵MST
反例:
可行的证明:
在不增加总权重的前提下,可以将任一MST转换为T,每一
2. Prim算法:实现
于是套用PFS框架,为将
扩充至 ,只需 选出优先级最高的跨边 及其对应顶点 ,并将其加入 随后,更新 中所有顶点的优先级(数) 注意:优先级数随后可能改变(降低)的顶点,必与 邻接 因此,只需枚举 的每一邻接顶点 ,并取 以上完全符合PFS的框架,唯一要做的工作无非是按照 prioUpdater()规范,编写一个优先级(数)更新器...
xxxxxxxxxx// Priority Updater ~ PrimPUg->pfs( 0, PrimPU<char, Rank>() ); //从顶点0出发,启动Prim算法template <typename Tv, typename Te> struct PrimPU { //Prim算法的顶点优先级更新器 virtual void operator()( Graph<Tv, Te>* g, Rank v, Rank u ) { if ( UNDISCOVERED != g->status(u) ) return; //对v的每个尚未被发现的邻居u,按 if ( g->priority(u) > g->weight(v, u) ) { //Prim g->priority(u) = g->weight(v, u); //策略 g->parent(u) = v; //做松弛 } }};
10.8 Kruskal算法
贪心原则: 根据代价,从小到大依次尝试各边 只要“安全”就加入该边 (每步局部最优 =全局最优)
1. 正确性
定理:Kruskal引入的每条边都属于某棵MST
设:边
Kruskal算法过程中不断生长的森林,总是某棵MST的子图
2. 并查集
Union-Find问题: 给定一组互不相交的等价类 各由其中一个成员作为代表
Find(x):找到元素x所属等价类Union(x, y):合并x和y所属等价类Singleton:初始时各包含一个元素Kruskal = Union-Find
- 查询:沿着树向上移动,直至找到根节点
- 路径压缩:查询过程中经过的每个元素都属于该集合,将其直接镰刀根节点以加快后续查询
- 合并:将一棵树的根节点连到另一棵树的根节点 启发式合并:选择哪棵树的根节点作为新树的根节点会影响未来操作的复杂度,我们可以将节点较少或深度较小的树连到另一棵,以免发生退化
- 删除:将删除的叶子节点的父亲设为自己。(制作副本)
- 移动:通过以副本作为父亲,保证要移动的元素都是叶子。
11 优先级队列
xxxxxxxxxxtemplate <typename T> struct PQ { // priority queue virtual void insert(T) = 0; virtual T getMax() = 0; virtual T delMax() = 0;};stack和queue都是PQ的特例——优先级完全取决于元素的插入次序 steap和queap也都是PQ的特例——插入和删除的位置受限
引入
1. Vector
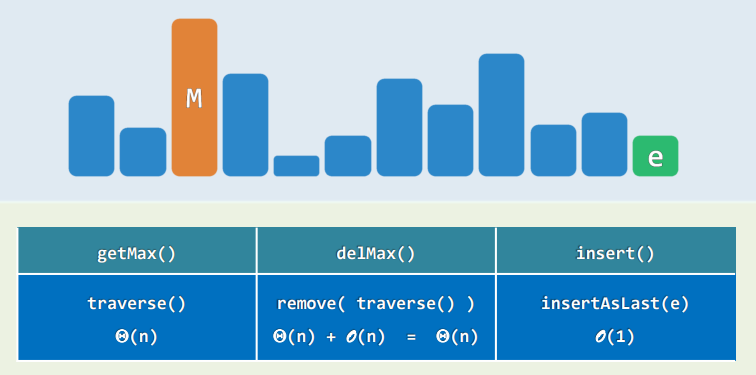
Sorted Vector:

2. List
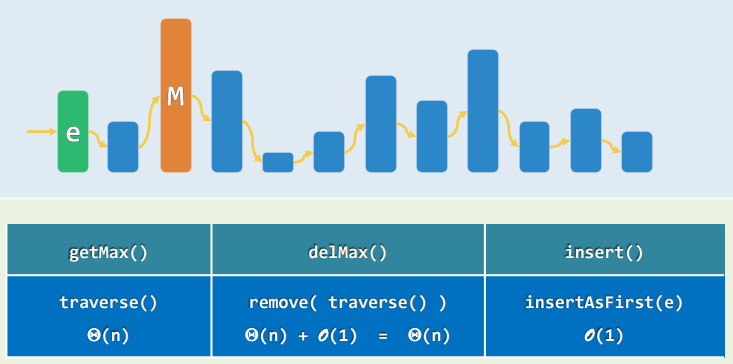
Sorted List:
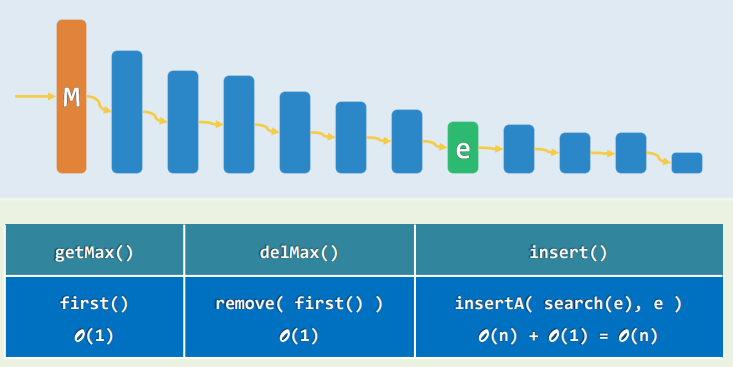
3. BBST
AVL、Splay、Red-black:三个接口均只需
但是BBST的功能远远超出了PQ的需求: 若只需查找极值元,则不必维护所有元素之间的全序关系,偏序足矣 因此有理由相信,存在某种更为简单、维护成本更低的实现方式
11.1 完全二叉堆
结构性:逻辑元素、物理节点依层次遍历次序彼此对应
逻辑上等同于完全二叉树
物理上直接借助向量实现
内部节点的最大秩 =
xxxxxxxxxx
PQ_ComplHeap = PQ + Vector
xxxxxxxxxxtemplate <typename T> struct PQ_ComplHeap : public PQ<T>, public Vector<T> { PQ_ComplHeap( T* A, Rank n ) { copyFrom( A, 0, n ); heapify( _elem, n ); } void insert( T ); T getMax() {return _elem[0];} T delMax();};template <typename T> Rank percolateDown( T* A, Rank n, Rank i ); //下滤template <typename T> Rank percolateUp( T* A, Rank i ); //上滤template <typename T> void heapify( T* A, Rank n); //Floyd建堆算法堆序性:只要
1. 插入
算法:逐层上滤
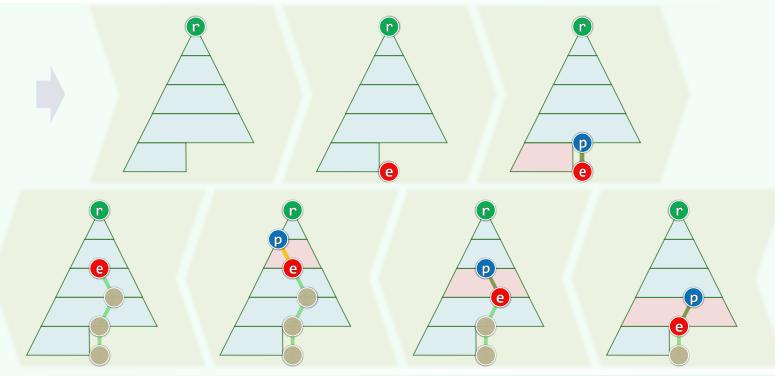
xxxxxxxxxxtemplate <typename T> void PQ_ComplHeap<T>::insert( T e ) { Vector<T>::insert( e ); percolateUp( _elem, _size - 1 ); } //此insert()非彼
template <typename T> Rank percolateUp( T* A, Rank i ) { //0 <= i < _size while ( 0 < i ) { //在抵达堆顶之前,反复地 Rank j = Parent( i ); //考查[i]之父亲[j] if ( lt( A[i], A[j] ) ) break; //一旦父子顺序,上滤旋即完成;否则 swap( A[i], A[j] ); i = j; //父子换位,并继续考查上一层 } //while return i; //返回上滤最终抵达的位置}效率:
e在上滤过程中,只可能与祖先们交换 完全树必平衡,e的祖先不超过
个,因此时间复杂度在 内 然而,就数学期望而言,实际效率往往远远更高
2. 删除
算法:割肉补疮 + 逐层下滤
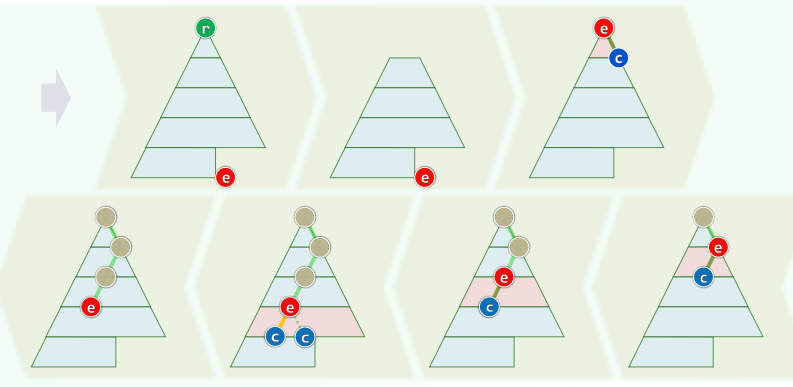
xxxxxxxxxxtemplate <typename T> T PQ_ComplHeap<T>::delMax() { //删除 T maxElem = _elem[0]; _elem[0] = _elem[ --_size ]; //摘除堆顶,代之以末词条 percolateDown( _elem, _size, 0 ); //对新堆顶实施下滤 return maxElem; //返回此前备份的最大词条}template <typename T> Rank percolateDown( T* A, Rank n, Rank i ) { //0 <= i < n Rank j; //i及其(至多两个)孩子中,堪为父者 while ( i != ( j = ProperParent( A, n, i ) ) ) //只要i非j,则 { swap( A[i], A[j] ); i = j; } //换位,并继续考察i return i; //返回下滤抵达的位置(亦i亦j)}效率:
e在每一高度至多交换一次,累计交换不超过
次 通过下滤,可在 时间内 删除堆顶节点,并整体重新调整为堆 然而,就数学期望而言,实际效率往往远远更高
3. 批量建堆
蛮力算法:
xxxxxxxxxx// 自上而下的上滤PQ_ComplHeap( T* A, Rank n ) { copyFrom( A, 0, n ); heapify( _elem, n ); }template <typename T> void heapify( T* A, const Rank n ) { //蛮力 for ( Rank i = 1; i < n; i++ ) //按照逐层遍历次序逐一 percolateUp( A, i ); //经上滤插入各节点}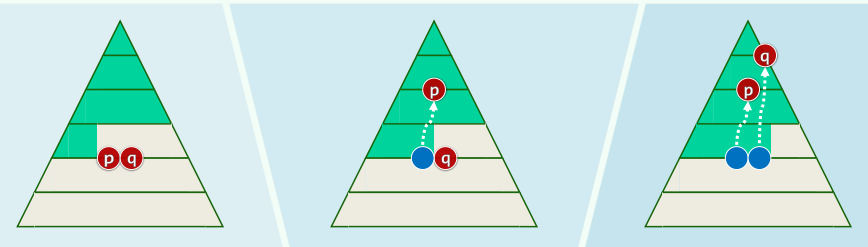
Worst Case =
自下而上的下滤:
任意给定堆
和 ,以及节点P 未得到堆 ,只需将 和 当作p的孩子,再对p下滤
xxxxxxxxxxtemplate <typename T> //Robert Floyd,1964void heapify( T* A, Rank n ) { //自下而上 for ( Rank i = n/2 - 1; 0 <= i; i-- ) //依次(从最后一个内部节点) percolateDown( A, n, i ); //下滤各内部节点} //可理解为子堆的逐层合并,堆序性最终必然在全局恢复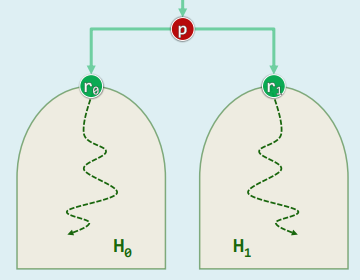
Example:
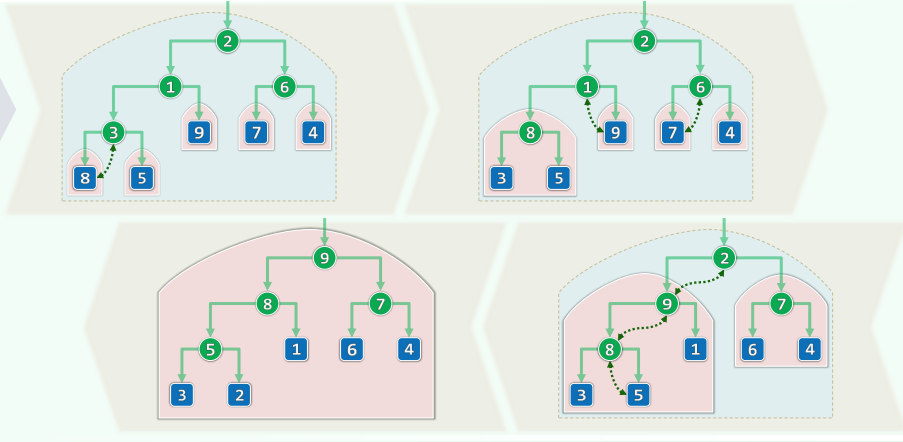
效率:
每个内部节点所需的调整时间,正比于其高度而非深度 不失一般性,考察满树:
所有节点的高度总和:
算法优化的本质:堆结构“深度”和“高度”的不确定性。采用高度累计减少复杂度。
课后思考:

11.2 堆排序
对比选择排序
SelectionSort(): 初始化:heapify(),迭代: delMax(),不变性:
——J. Williams, 1964
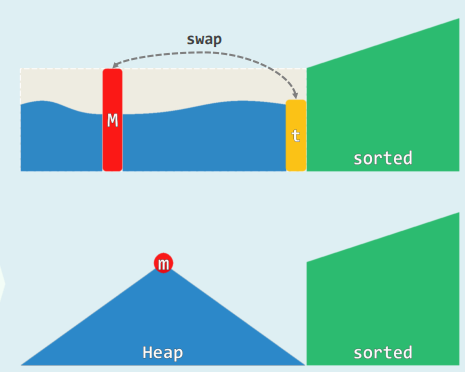
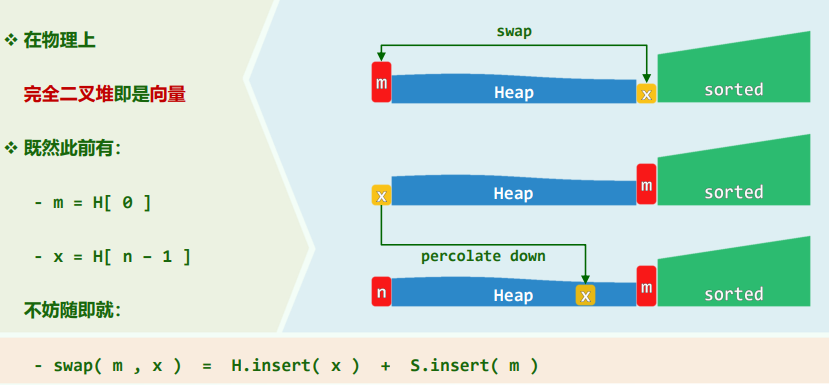
xxxxxxxxxxtemplate <typename T> //对向量区间[lo, hi)做就地堆排序void Vector<T>::heapSort( Rank lo, Rank hi ) { T* A = _elem + lo; Rank n = hi - lo; heapify( A , n ); //待排序区间建堆,O(n) while ( 0 < --n ) //反复地摘除最大元并归入已排序的后缀,直至堆空 { swap( A[0], A[n] ); percolateDown( A, n, 0 ); } //堆顶与末元素对换后下滤}1. 锦标赛树:胜者树
完全二叉树 叶节点:待排序元素(选手) 内部节点:孩子中的胜者 树根总是全局冠军:类似于堆顶 内部结点各对应于一场比赛的胜者——重复存储
create():remove():insert():
Tournamentsort()CREATE a tounament tree for the input list while there are active leaves RMOVE the root RETRACE the root down to its leaf DEACTIVATE the leaf REPLAY along the path back to the root
效率:
空间:
选取:从n个元素中找出最小的k个
初始化:
渐进意义上确实如此,但就常系数而言,区别不小
Floyd算法,delMax()中的percolateDown()在每一层需做2次比较,累计大致次
2. 锦标赛树:败者树
内部节点记录对应比赛的败者 增设根的“父节点”,记录冠军 ——这样的算法设计是因为胜者树的REPLAY涉及“找兄弟比赛”的过程(时间上就有消耗) 而采用败者树REPLAY时每次的比赛只需要找父亲即可
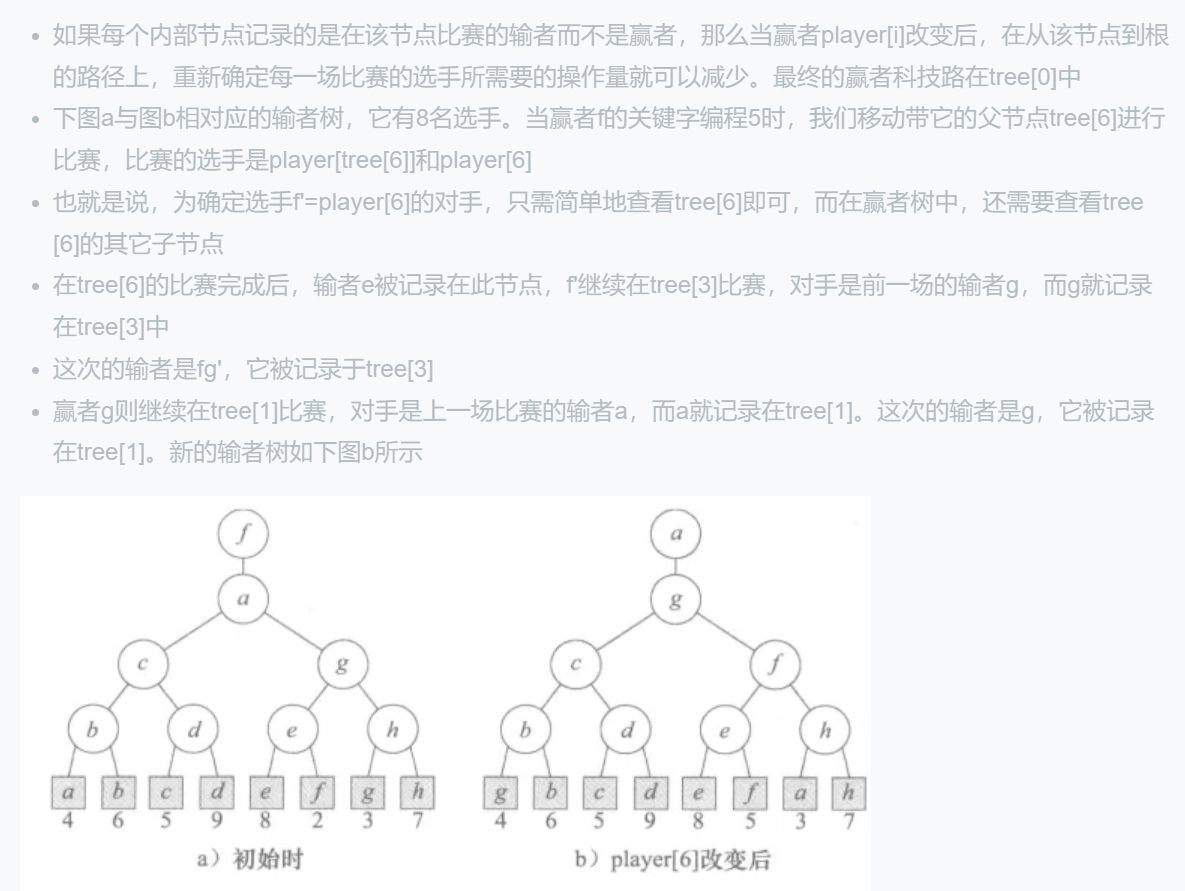
11.3 多叉堆
背景:优先级搜索(例如Prim和Dijkstra算法)中,若采用邻接表,更新优先级和选出优先级最高者的累计时间分别为
和 。能否更快?
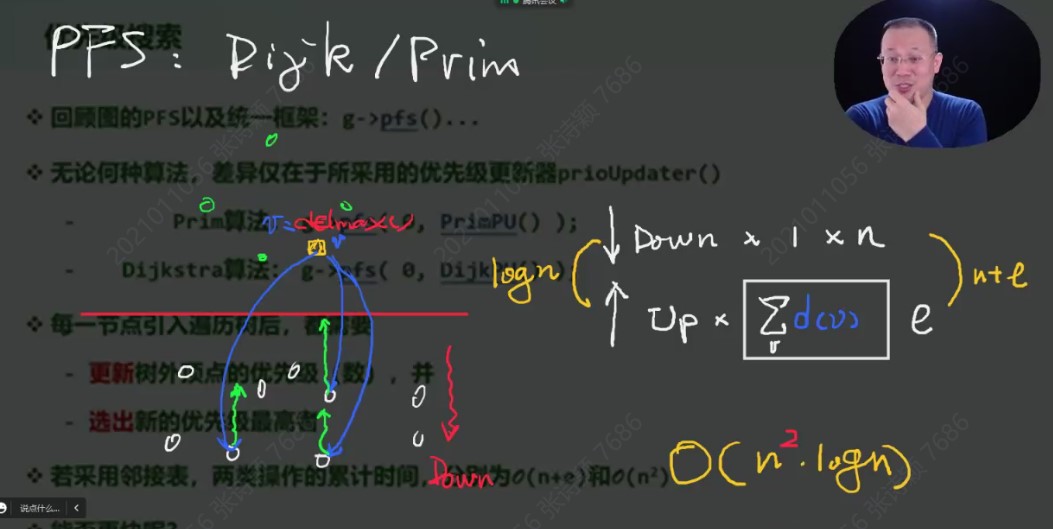
优先级队列对pfs的改进
PFS中的各顶点可以组织为优先级队列 为此需要使用PQ接口:
heapify():由n个顶点创建初始PQ,总计delMax():取优先级最高 / 极短跨边(u, w),总计increase():更新所有关联顶点到u的距离,提高优先级,总计总体运行时间 = 对于稀疏图,处理效率很高 对于稠密图,反而不如常规实现的版本
多叉堆多优先级队列的改进
给予Vector实现,父子节点的秩可以简明地互相换算
heapify():,不可能再快了 delMax():,实质就是 perculateDown(),已是极限increase():,实质就是 perculateUp(),还有改进空间...
将二叉堆改成多叉堆(d-heap):
堆高度降至perculateUp()成本降至perculateDown()成本增至(只要
则此时PFS时间复杂度为
对于稀疏图保持高效:
11.4 左式堆
1. 堆合并
方法一:A.insert(B.delMax())
union(A, B).heapify(n + m)
二堆合并 = 二路归并
放弃“完全性”(completeness),保留“堆序性”
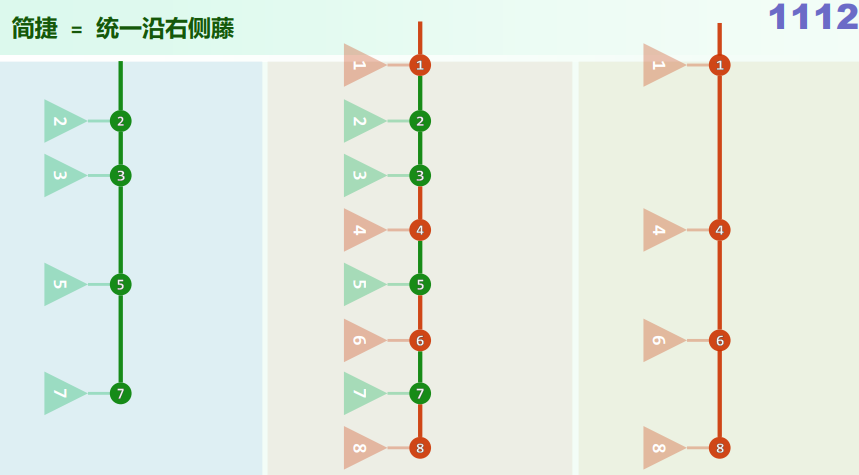
递归实现:所需时间正比于右侧藤总长
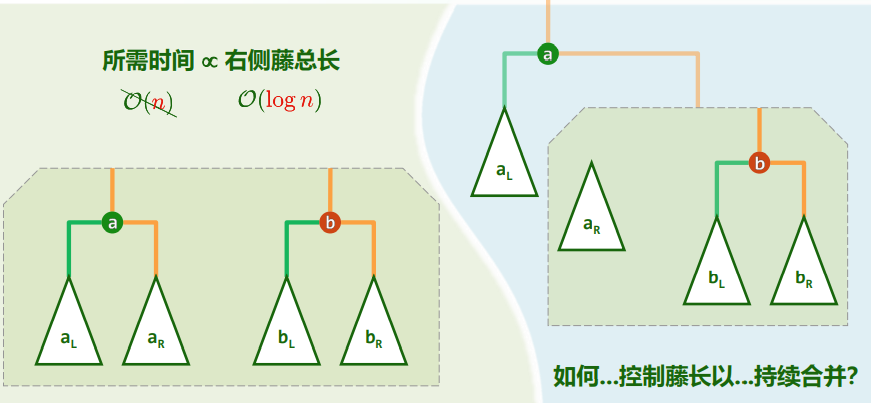
2. NPL与控制藤长
C. A. Crane, 1972: 保持堆序性,附加新条件,使得在堆合并过程中,只涉及少量节点:
新条件 = 单侧倾斜: 节点分布偏向左侧 合并操作只涉及右侧
空节点路径长度
引入所有的外部节点 消除一度节点,转为真二叉树
Null Path Length
验证:
左式堆
对任何内节点x,都有:
左倾性与堆序性,相容而不矛盾 左式堆的子堆必然也是左式堆 左式堆倾向于更多节点分布于左侧分支
右侧链
右侧链长为d的左式堆,至少包含
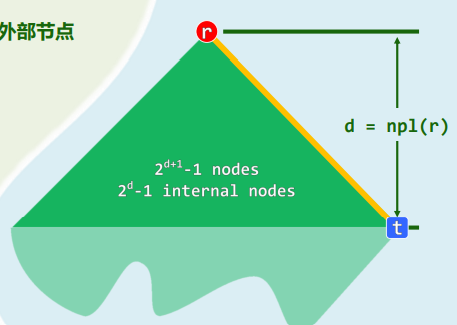
3. 合并算法
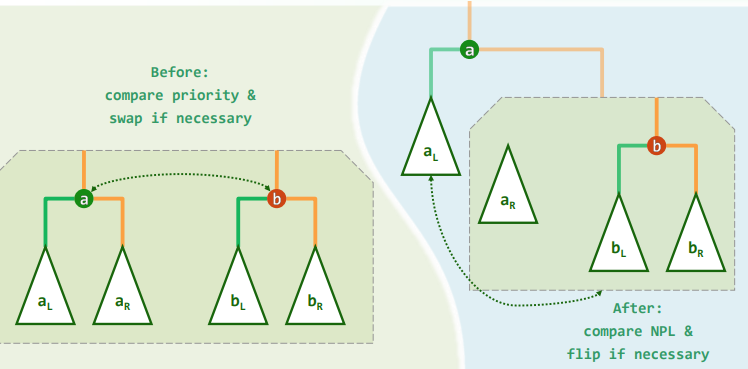
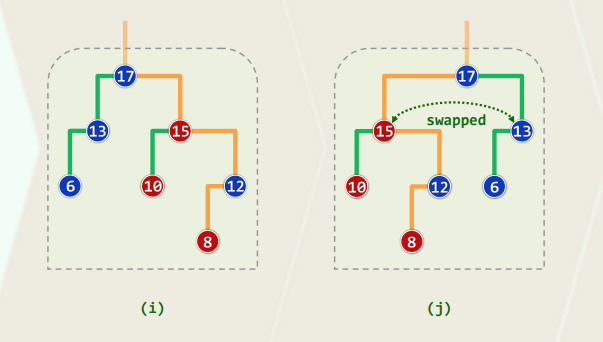
xxxxxxxxxxtemplate <typename T> //基于二叉树,以左式堆形式实现的优先级队列class PQ_LeftHeap : public PQ<T>, public BinTree<T> {public: T getMax() { return _root->data; } void insert(T); T delMax(); //均基于统一的合并操作实现... PQ_LeftHeap( PQ_LeftHeap & A, PQ_LeftHeap & B ) { _root = merge(A._root, B._root); _size = A._size + B._size; A._root = B._root = NULL; A._size = B._size = 0; }};
template <typename T> BinNodePosi<T> merge(BinNodePosi<T> a, BinNodePosi<T> b) { if ( !a ) return b; if ( !b ) return a; //递归基 if ( lt( a->data, b->data ) ) swap( a, b ); //确保a>=b ( a->rc = merge( a->rc, b ) )->parent = a; //将a的右子堆,与b合并 if ( ! a->lc || a->lc->npl < a->rc->npl ) //若有必要 swap( a->lc, a->rc ); //交换a的左、右子堆,以确保左子堆的npl不小 a->npl = a->rc ? 1 + a->rc->npl : 1; //更新a的npl return a; //返回合并后的堆顶}
//迭代实现template <typename T> BinNodePosi<T> merge( BinNodePosi<T> a, BinNodePosi<T> b ) { if ( !a ) return b; if ( !b ) return a; //退化情况 if ( lt( a->data, b->data ) ) swap( a, b ); //确保a>=b for ( ; a->rc; a = a->rc ) //沿右侧链做二路归并,直至堆a->rc先于b变空 if ( lt( a->rc->data, b->data ) ) { b->parent = a; swap( a->rc, b); } //接入b (a->rc = b)->parent = a; //直接接入b的残余部分(必然非空) for ( ; a; b = a, a = a->parent ) { //从a出发沿右侧链逐层回溯(b == a->rc) if ( !a->lc || a->lc->npl < a->rc->npl ) swap( a->lc, a->rc ); //确保npl合法 a->npl = a->rc ? a->rc->npl + 1 : 1; //更新npl } return b; //返回合并后的堆顶} 4. 插入与删除
插入
xxxxxxxxxxtemplate <typename T>void PQ_LeftHeap<T>::insert( T e ) { //O(logn)_root = merge( _root, new BinNode<T>( e, NULL ) );_size++;}删除
xxxxxxxxxxtemplate <typename T>T PQ_LeftHeap<T>::delMax() { //O(logn)BinNodePosi<T> lHeap = _root->lc; if (lHeap) lHeap->parent = NULL;BinNodePosi<T> rHeap = _root->rc; if (rHeap) rHeap->parent = NULL;T e = _root->data;delete _root; _size--;_root = merge( lHeap, rHeap );return e;}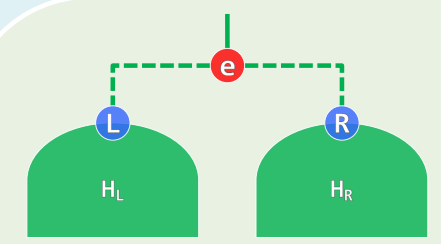
12 串
12.1 模式匹配
Text: 串,长度记为
Pattern: 模式子串,长度记为 记字符集为 ,则字符集的个数
蛮力算法:
Best Case:
Version 1:
xxxxxxxxxxint match( char * P, char * T ) { size_t n = strlen(T), i = 0; size_t m = strlen(P), j = 0; while ( j < m && i < n ) //自左向右逐次比对 if ( T[i] == P[j] ) { i++; j++; } //若匹配,则转到下一对字符 else { i -= j - 1; j = 0; } //否则,T回退、P复位 return i - j; //最终的对齐位置:藉此足以判断匹配结果}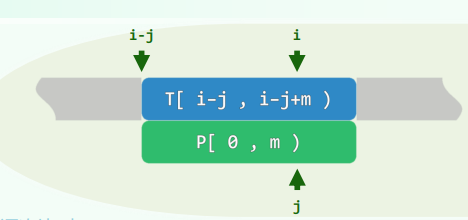
Version 2:
xxxxxxxxxxint match( char * P, char * T ) { size_t n = strlen(T), i = 0; size_t m = strlen(P), j; for ( i = 0; i < n - m + 1; i ++ ) { //T[i]与P[0]对齐后 for ( j = 0; j < m; j ++ ) //逐次比对 if ( T[i + j] != P[j] ) break; //失配,转下一对齐位置 if ( m <= j ) break; //完全匹配(Python:可以写得更简洁、优美)} return i; //最终的对齐位置:藉此足以判断匹配结果}1. KMP算法
在任意时刻,都有
此时,我们已经掌握了 的所有信息 因此,一旦失败,就应该已知哪些位置值得/不必对齐,则在下一轮比对中, 可直接接收,而不必再做比对
由此,i将永远不必回退 比对成功,则与j同步前进一个字符 否则,j更新为某一更小的t,比继续比对
优化 = P可快速右移 + 避免重复比对
提问:为确定t,需花费多少时间和空间?更重要的,可否在事先就确定?
查询表
t:不仅可以事先确定,而且仅根据
即可确定 视失败的位置j,无非m种情况 构造查询表 ,做好预案 一旦在 处失配,只需将j替换为 ,继续与 比对
串首补齐一个通配符(
*)
xxxxxxxxxxint match( char * P, char * T ) { int * next = buildNext(P); int n = (int) strlen(T), i = 0; int m = (int) strlen(P), j = 0; while ( j < m && i < n ) if ( 0 > j || T[i] == P[j] ) { i++; j++; } else j = next[j]; delete [] next; return i - j;}快速右移,绝不回退:
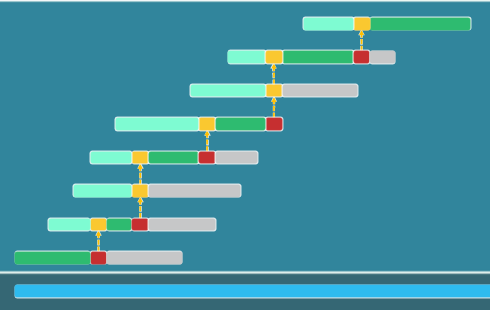
next表
P在t处自匹配 长度最大,位移最小,不致日后回溯
传递链:动态规划
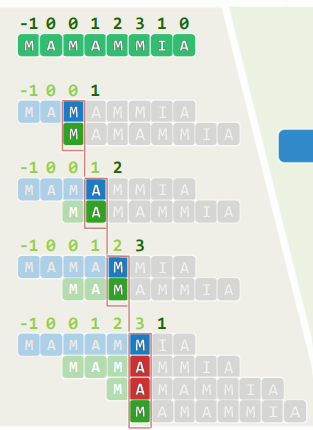
xxxxxxxxxxnext[j + 1] = next[j] + 1 iff P[j] = P[next[j]]xxxxxxxxxxint * buildNext( char * P ) { size_t m = strlen(P), j = 0; int *N = new int[m]; int t = N[0] = -1; while ( j < m - 1 ) ( 0 > t || P[j] == P[t] ) ? N[ ++j ] = ++t : t = N[t]; return N;}分摊分析
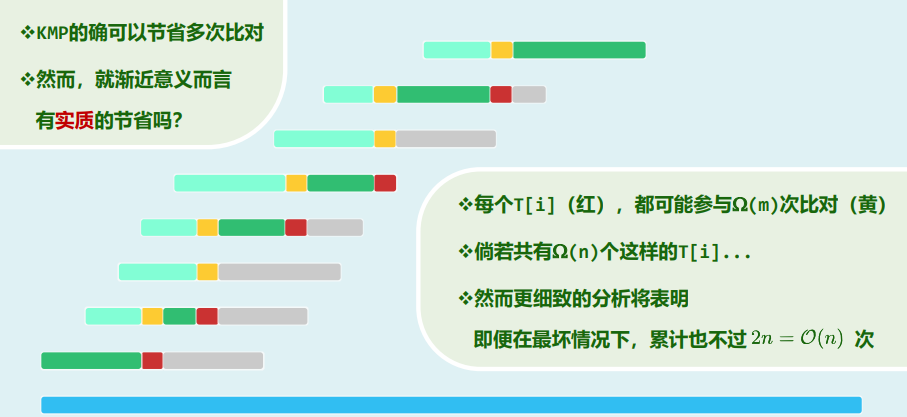
尽管如此,“黄色块”不会一直出现,其总的分摊复杂度并不高
while循环前,令计步器k = 2 * i - j(初始有k = 0),代表迭代步数的上界
则算法结束时:
因此,总体时间复杂度为
再分析
反例
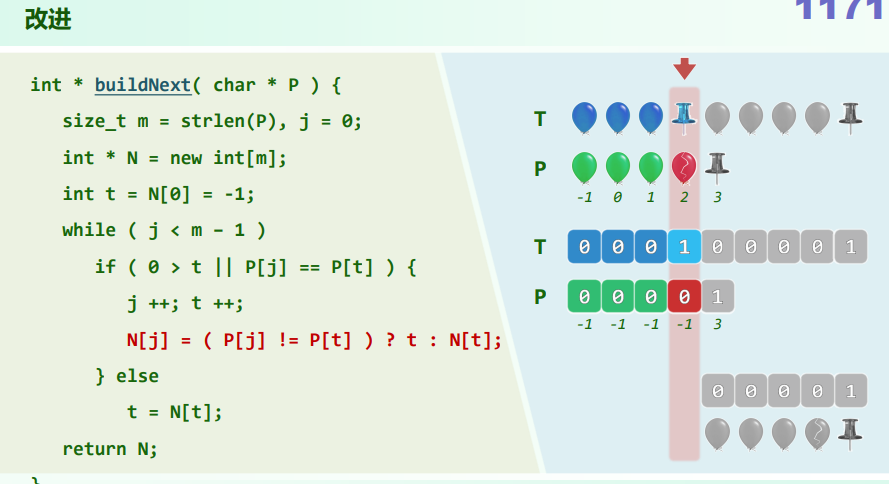
渐近复杂度仍然是线性的。
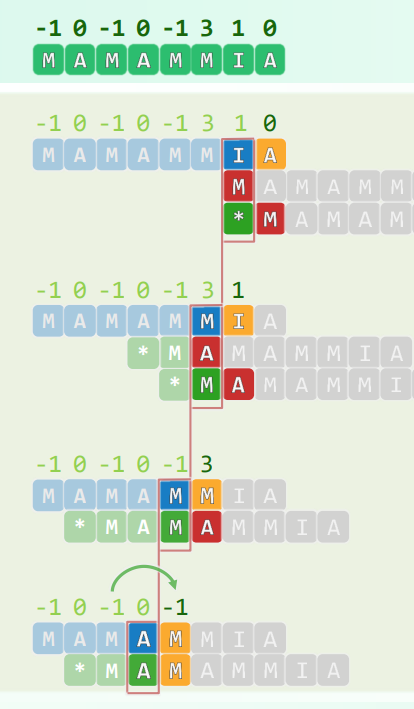
小结:
充分利用以往的比对所提供的信息:模式串快速右移,文本串无需回退
经验 ~ 以往成功的比对:
2. BM算法
BC策略:以终为始
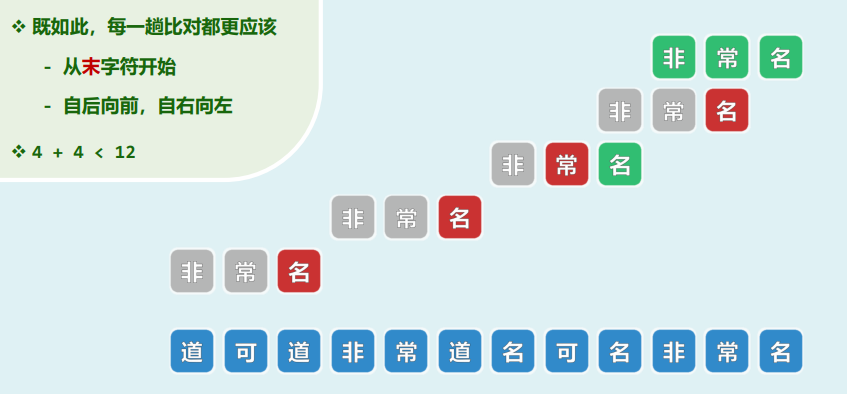
自左向右移动P,自右向左比对P和T
Boyer + Moore, 1977: A Fast String Searching Algorithm 预处理:根据模式串P,预先构造
gs[]表和bc[]表 迭代:自右向左依次比对字符,找到极大的匹配后缀 若完全匹配,则返回位置; 否则,查表确定P右移的适当位置,并重新自右向左比对
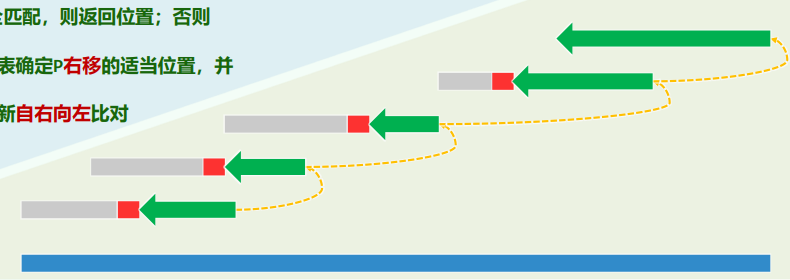
坏字符

构造bc[]:画家算法
xxxxxxxxxxint* buildBC(char* P) { int* bc = new int[256]; for (size_t j = 0; j < 256; ++j) bc[j] = -1; for (size_t m = strlen(P), j = 0; j < m; ++j) bc[P[j]] = j; // painter's algorithm return bc;} // O(s + m)
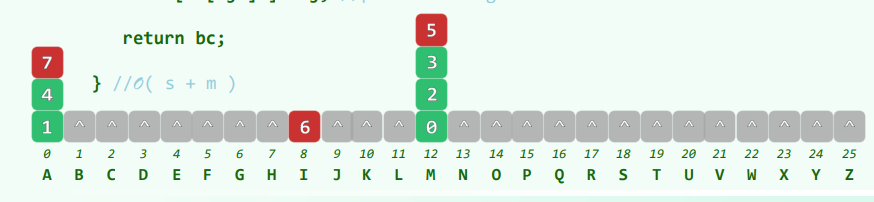
性能分析:
最好情况:

最差情况:

每轮迭代,都要扫过整个P之后,方能确定右移一个字符 此时,须经m次比较,方能排除单个对齐位置 单词匹配概率越大的场合,性能越接近于蛮力算法(小字母表Bitmap + DNA) 反思:借助以上
bc[]表,仅仅利用了失配比对提供的信息(教训) 类比:可否仿照KMP,同时利用起匹配比对提供的信息(经验)?
GS策略:好后缀

[EG]:
构造gs[]表
BC+GS综合性能
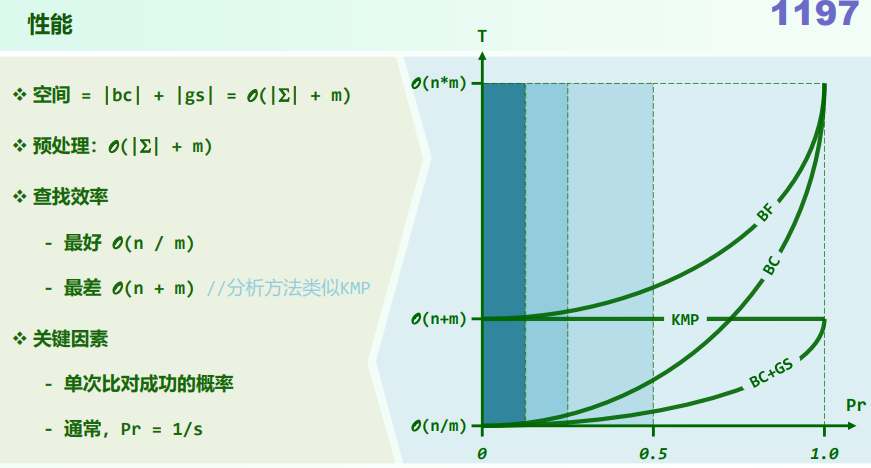
3. Karp-Rabin算法:串即是数
凡物皆数:Godel Numbering 逻辑系统的符号、表达式、公式、命题、定理、公理等,均可表示为自然数 每个有限维的自然数向量(包括字符串),都唯一对应于某个自然数
素数序列:
若果真如RAM模型所假设的字长无限,则只需一个寄存器即可...
凡物皆数:Cantor Numbering
十进制串,可直接视作自然数:指纹(fingerprint),等效于多项式法
//设d = |∑|
于是,每个字符串都对应于一个 d 进制自然数 //尽管不是单射
//∑ = { A, B, C, ..., Z }
散列
基本构思:通过对比经压缩之后的指纹,确定匹配位置 关键技巧:通过散列,将指纹压缩至存储器支持的范

注意:通过hash()筛选后,还需经过严格的比对,方可最终确定是否匹配
适当选取散列函数,可以极大降低冲突的概率
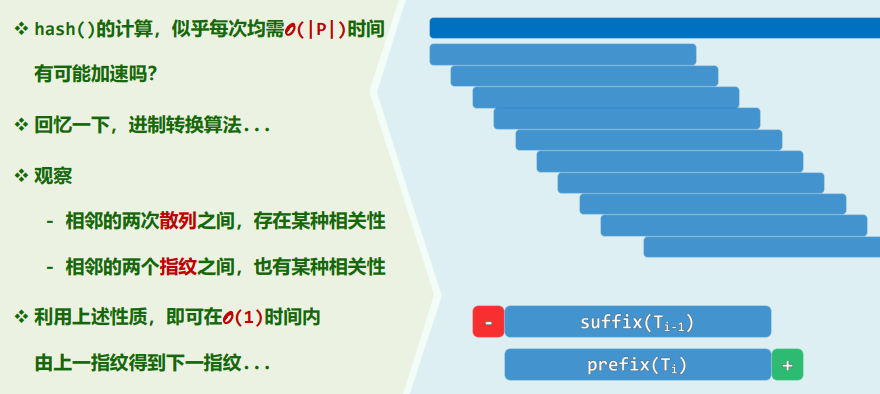
字宽


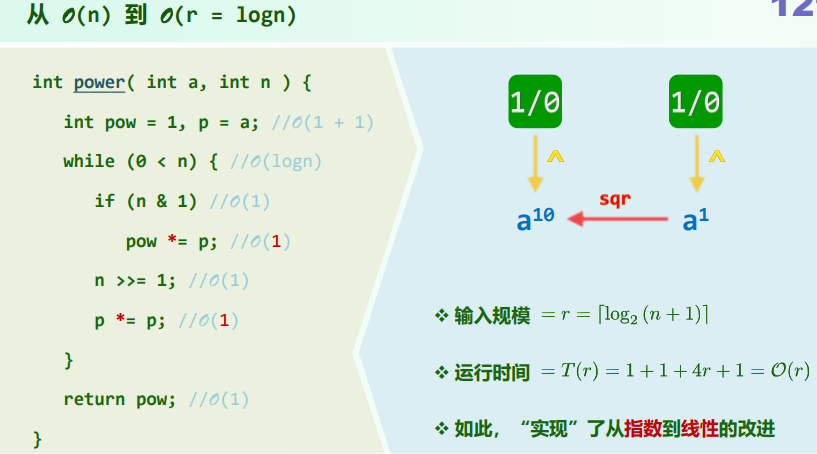
只对n比较小的时候成立
再分析

12.2 键树 Trie
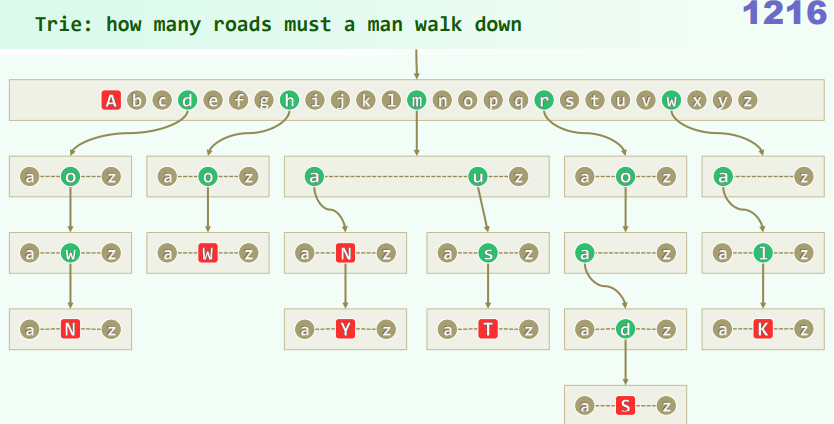
其中,红色的节点表示单词的结束节点(不一定是叶子结点)
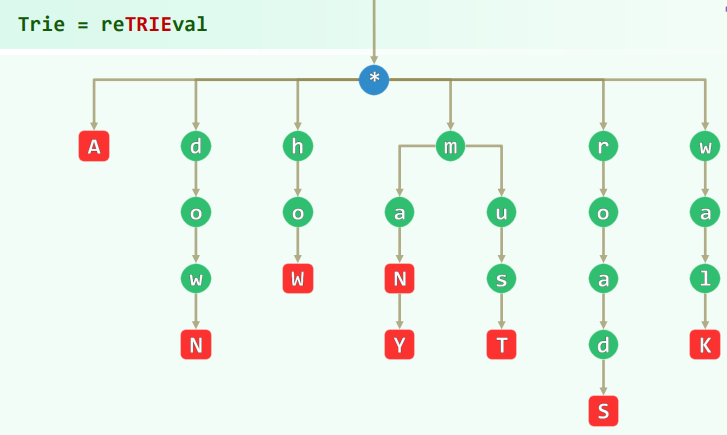
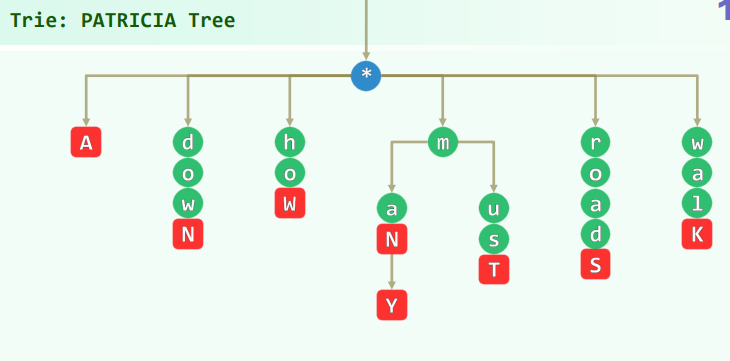
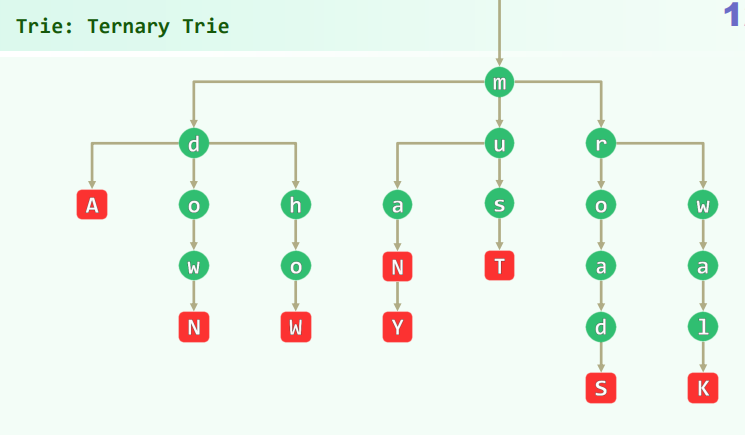
13 排序
13.1 快速排序
C. A. R. Hoare:分而治之 pivot:左侧/右侧的元素,均不比它更大/更小 以轴点为界,自然划分:
前缀、后缀各自递归排序之后,原序列自然有序: mergesort难点在于合,quicksort在于分 通过培养轴点来实现上述划分
快速排序就是将所有元素逐个转换为轴点的过程
xxxxxxxxxxtemplate <typename T>void Vector<T>::quickSort(Rank lo, Rank hi) { if (hi - lo < 2) return; Rank mi = partition(lo, hi); quickSort(lo, mi); quickSort(mi + 1, hi);}快速划分:LUG版
任选一个候选者(如[0]),交替地向内移动lo和hi
逐个检查当前元素:若更小/大,则转移归入L/G
当
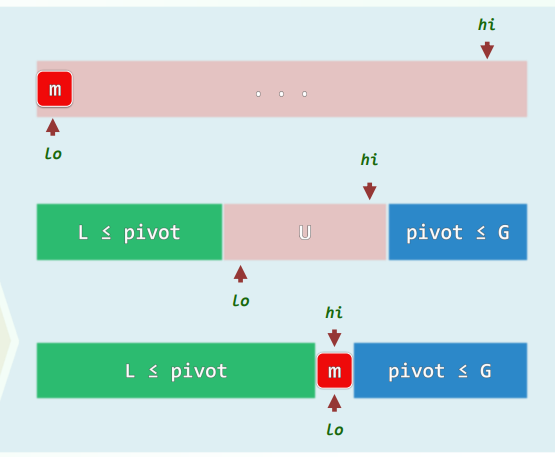
xxxxxxxxxxtemplate <typename T> Rank Vector<T>::partition( Rank lo, Rank hi ) { //[lo, hi) swap(_elem[lo], _elem[lo + rand() % (hi - lo)]); //随机交换 T pivot = _elem[lo]; //经以上交换,等效于随机选取候选轴点 while (lo < hi) { //从两端交替地向中间扫描,彼此靠拢 do {hi--;} while (lo < hi && pivot <= _elem[hi]); //向左拓展G if (lo < hi) _elem[lo] = _elem[hi]; //凡小于轴点者,皆归入L do {lo++;} while (lo < hi && _elem[lo] <= pivot); //向右拓展L if (lo < hi) _elem[hi] = _elem[lo]; //凡大于轴点者,皆归入G } //assert: lo == hi or hi + 1 _elem[hi] = pivot; return hi; }不变性 + 单调性:[lo]和[hi]交替空闲
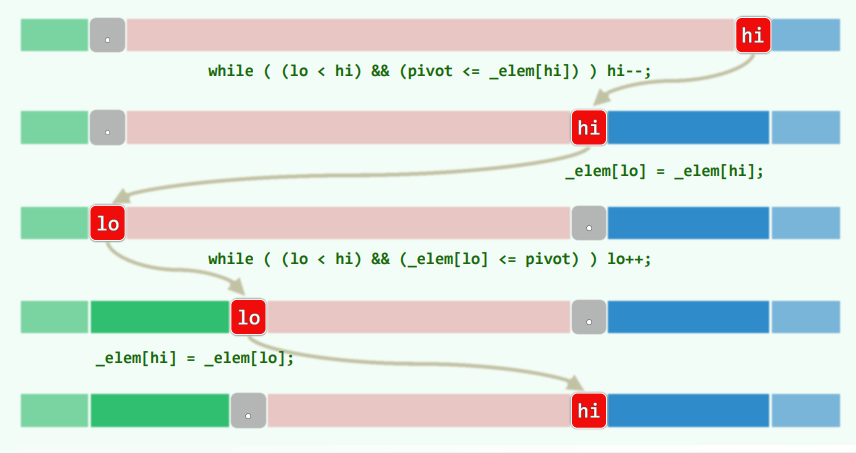
复杂度分析:
线性时间:尽管lo, hi交替移动,累计移动距离不过lo/hi的移动方向相反,左/右侧的大/小重读元素可能前/后颠倒
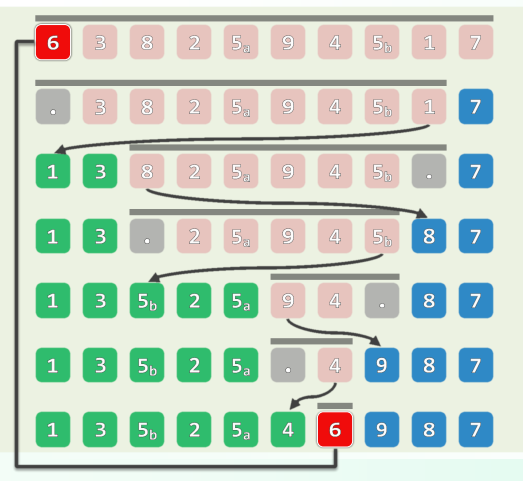
2. 迭代、贪心与随机
空间复杂度 ~ 递归深度
最好:划分总是均衡
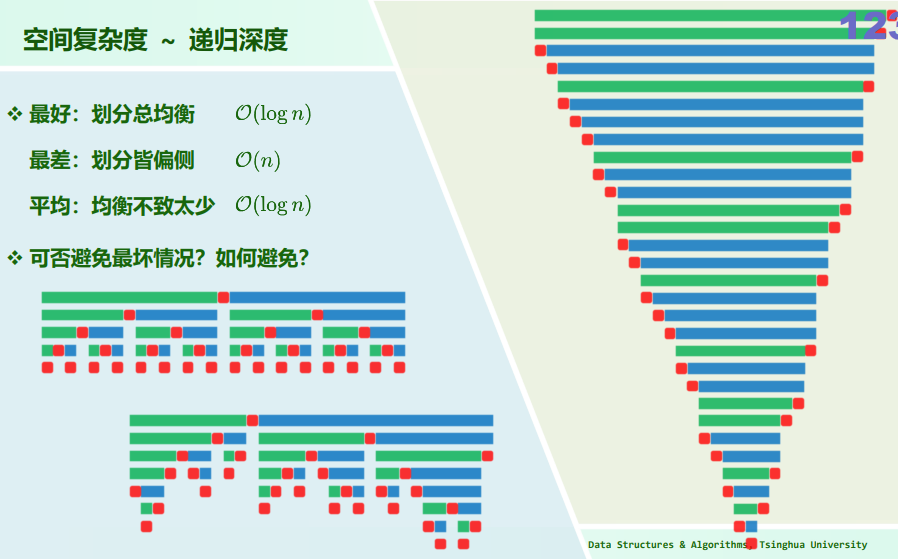
非递归 + 贪心
保证递归深度可能超过
xxxxxxxxxxtemplate <typename T> void Vector<T>::quickSort( Rank lo, Rank hi ) { Stack<Rank> Task; Put(Task, lo, hi); //等效于对递归树的先序遍历 while (!Task.empty()) { Get(Task, lo, hi); Rank mi = partition(lo, hi); if (mi - lo < hi - mi ) { Put(Task, mi + 1, hi); Put(Task, lo, mi); } else { Put(Task, lo, mi); Put(Task, mi + 1, hi); } } //大|小任务优先入|出栈,可保证(辅助栈)空间不过O(logn)}时间性能 + 随机
- 最好情况:每次划分都(接近)平均,轴点总是(接近)中央——到达下界
- 最坏情况:每次划分都极不均衡(比如,轴点总是最小/大元素)——与起泡排序相当
- 采用随机选取(Randomization),三者取中(Sampling)之类的策略 只能降低最坏情况的概率,而无法杜绝——既然如此,为何还称作快速排序?
3. 递归深度
最坏情况(
递归深度)概率极低 平均情况( 递归深度)概率极高
除非过于侧片的pivot,都会有效地缩短递归深度
准居中:pivot落在宽度为
期望深度
每递归一层,都有

4. 比较次数
move的次数一定不超过compare的次数
期望的比较次数为


后向分析:
设经排序后得到的输出序列为:
quickSort的过程及结果,可理解为:按某种次序,将各元素逐个确认为pivot
若

对比:
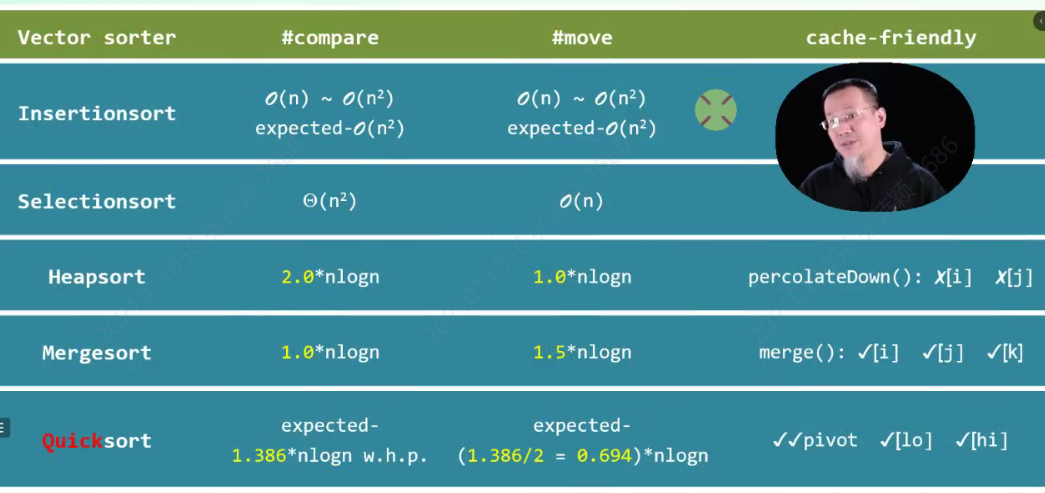
快读划分:DUP版
大量甚至全部元素重复时,轴点位置总是接近于
lo,子序列的划分极度失衡,二分递归退化为线性递归,递归深度接近于,运行时间接近于 移动
lo和hi的过程中,同时比较相邻元素若属于相邻的重复元素,则不再深入递归
LUG'版本:勤于拓展、懒于交换
xxxxxxxxxxtemplate <typename T> Rank Vector<T>::partition( Rank lo, Rank hi ) { //[lo, hi) swap( _elem[lo], _elem[lo + rand() % (hi – lo)] ); //随机交换 hi--; T pivot = _elem[lo]; //经以上交换,等效于随机选取候选轴点 while (lo < hi) { //从两端交替地向中间扫描,彼此靠拢 while (lo < hi && pivot <= _elem[hi]) hi--; //向左拓展G if (lo < hi) _elem[lo++] = _elem[hi]; //凡小于轴点者,皆归入L while (lo < hi && _elem[lo] <= pivot) lo++; //向右拓展L if (lo < hi) _elem[hi--] = _elem[lo]; //凡大于轴点者,皆归入G } //assert: lo == hi _elem[lo] = pivot; return lo; //候选轴点归位;返回其秩}DUP'版本
xxxxxxxxxxtemplate <typename T> Rank Vector<T>::partition( Rank lo, Rank hi ) { //[lo, hi) swap( _elem[lo], _elem[lo + rand() % (hi – lo)] ); //随机交换 hi--; T pivot = _elem[lo]; //经以上交换,等效于随机选取候选轴点 while (lo < hi) { //从两端交替地向中间扫描,彼此靠拢 while (lo < hi && pivot < _elem[hi]) hi--; //向左拓展G if (lo < hi) _elem[lo++] = _elem[hi]; //凡不大于轴点者,皆归入L while (lo < hi && _elem[lo] < pivot) lo++; //向右拓展L if (lo < hi) _elem[hi--] = _elem[lo]; //凡不小于轴点者,皆归入G } //assert: lo == hi _elem[lo] = pivot; return lo; //候选轴点归位;返回其秩}DUP版本:懒于拓展、勤于交换
xxxxxxxxxxtemplate <typename T> Rank Vector<T>::partition( Rank lo, Rank hi ) { //[lo, hi) swap( _elem[lo], _elem[lo + rand() % (hi – lo)] ); //随机交换 hi--; T pivot = _elem[lo]; //经以上交换,等效于随机选取候选轴点 while (lo < hi) { //从两端交替地向中间扫描,彼此靠拢 while (lo < hi) if (pivot < _elem[hi]) hi--; //向左拓展G,直至遇到不大于轴点者 else { _elem[lo++] = _elem[hi]; break; } //将其归入L while ( lo < hi ) if (_elem[lo] < pivot) lo++; //向右拓展L,直至遇到不小于轴点者 else { _elem[hi--] = _elem[lo]; break; } //将其归入G } //assert: lo == hi _elem[ lo ] = pivot; return lo; //候选轴点归位;返回其秩}快速化分:LGU版
不变性:
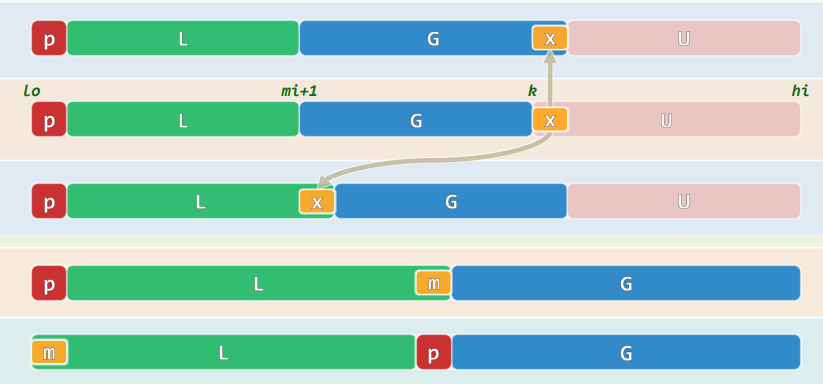
单调性:
xxxxxxxxxxtemplate <typename T> Rank Vector<T>::partition( Rank lo, Rank hi ) { //[lo, hi) swap( _elem[lo], _elem[lo + rand() % ( hi – lo )] ); //随机交换 T pivot = _elem[lo]; int mi = lo; for ( Rank k = lo + 1; k < hi; k++ ) //自左向右考查每个[k] if ( _elem[k] < pivot ) //若[k]小于轴点,则将其 swap( _elem[++mi], _elem[k]); //与[mi]交换,L向右扩展 swap( _elem[lo], _elem[mi] ); //候选轴点归位(从而名副其实) return mi; //返回轴点的秩}
13.2 快速选择 QuickSelect
xxxxxxxxxxtemplate <typename T> void quickSelect( Vector<T> & A, Rank k ) { for ( Rank lo = 0, hi = A.size() - 1; lo < hi; ) { Rank i = lo, j = hi; T pivot = A[lo]; //大胆猜测 while ( i < j ) { //小心求证:O(hi - lo + 1) = O(n) while ( i < j && pivot <= A[j] ) j--; A[i] = A[j]; while ( i < j && A[i] <= pivot ) i++; A[j] = A[i]; } //assert: quit with i == j A[i] = pivot; if ( k <= i ) hi = i - 1; if ( i <= k ) lo = i + 1; } //A[k] is now a pivot}期望性能
- 记期望的比较次数为
- 可以证明:
- 事实上,不难验证:
13.3 线性选择 LinearSelect

复杂度